How to find the limit?

Question

Mathematics

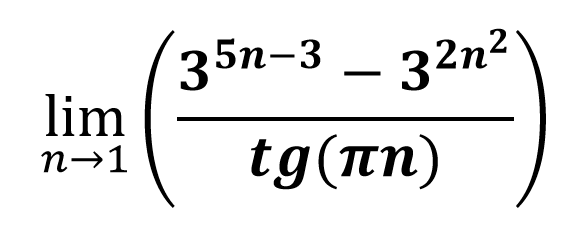
Please tell me how to solve, they said that it is impossible to use the L'Hopital rule, so there is not even a hint of a solution, please help

Answer 1

Replace n'=n-1. Take advantage of the fact that the period of the tangent is Pi, so the denominator will simply be tg(n'). Get the limit to n'->0.
Expand the tangent as the ratio of sine and cosine.
Now we need to screw something into the formula to get wonderful limits. For example, you can divide the numerator and denominator by pi*n. Then the denominator will be lim x->0: sin(x)/x, which is equal to 1. In the numerator, you can get lim x->0: (e^x - 1) / x = 1 twice: for this, each expression is 3 ^f(x) must be multiplied and divided by ln(3)*f(x) and add and subtract 1 in the numerator. Then you highlight 3 wonderful limits and in the end there should be no uncertainties left.