Answer the question
In order to leave comments, you need to log in
How to find the distance from the center as a percentage?
Given:
Image of known width and height (W, H).
Knowing W, H, it is easy to find the coordinates of the center of the image (imgCX = W / 2, imgCY = H / 2)
The image can contain an arbitrary number of rectangles. The coordinates of their vertices are known (x1y1...x4y4), as well as the coordinates of the center (rectCX, rectCY)
Based on the available data, we found the distance of each rectangle from the center of the image in pixels (S1) TO... (up to what?)
Actually the question is: How find the distance of each rectangle from the center of the image as a percentage?
I think I understand the algorithm: determine the angle for each vector S1, find the absolute distance (S2), calculate the percentage. But knowledge is not enough. Mathematicians, forgive me if the question seems noob :)
PS rectangles can be placed anywhere on the image.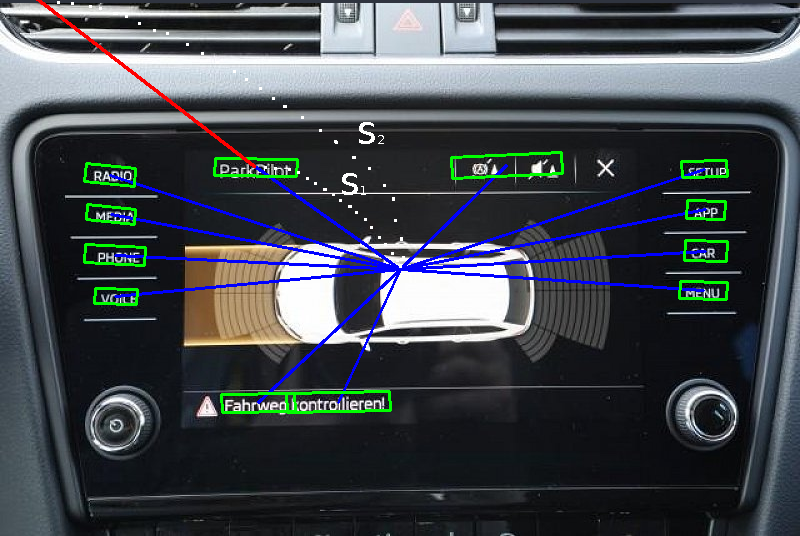
Answer the question
In order to leave comments, you need to log in
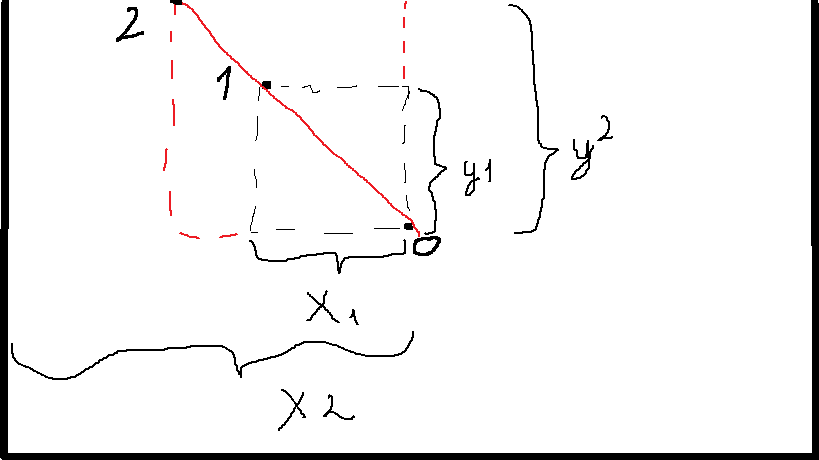
If we assume that 0 is the center, 1 is the middle of the rectangle, then you need to find one more point - 2. And then the length of the segment 01 / the length of the segment 02 = y1 / y2 = x1 / x2 (when point 2 is left or right). It turns out you can find one of the coordinates of point 2
As a percentage of what?
This is where you need to push back.
You don't need an angle.
For example, in the corners of the screen, the distance is maximum, 100%, and zero in the center.
Then the percentage distance will be 100*S(i)/maxDist
Where maxDist is the length of the diagonal from the center to the corner:
maxDist = sqrt(imgCX^2+imgCY^2) = sqrt(W*W/4+H*H/4)
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question