How to find ALL shortest paths between two vertices?

Question

Algorithms

How can you find all the shortest paths between two vertices in an undirected graph? The problem is this: there may be a situation when there are several shortest paths from some vertex u to the vertex v and they are all the same length. What to do in such a situation? Here is an example of such a graph: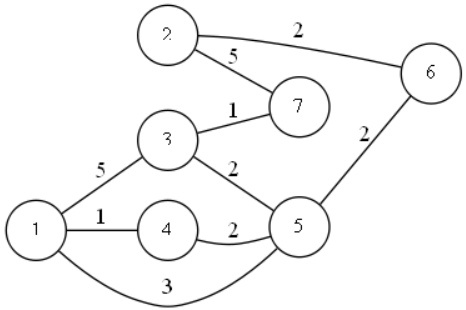
There are three shortest paths of the same length from node 1 to node 3: 1-3, 1-4-5-3, 1-5-3

Answer 1

What for?
Imagine a chessboard, your vertices are cells, edges are borders of adjacent cells and only them, transition step_left/step_right/step_up/step_down.
How many shortest paths are there from the bottom left cell to the top right? спойлер: 3432
And if you imagine a similar three-dimensional cube? 399072960
Conclusion: the task sucks set.
UPDATE
For clarity, let's say 3 faces come out of one of the desired vertices.
You build the shortest path, it passes through the first of 3 faces. You remember the path, you cut the line.
You build the shortest path, it passes through the second edge. If it is equal to the first one, you remember, you cut the second side, if it is more, you can completely throw out the second and third sides.
You get the first path, restore the first edge, follow the path further to the top with a fork. you cut the edge of the shortest path - well, of course, recursion.
On a degenerate graph, as I promised, Khan.

Answer 2

It seems to me that it is most convenient to use breadth-first traversal. Recording the weight and path to each encountered vertex.
At the end point, all options will be collected.
Only this thing will eat memory terribly and it would not hurt to make some optimizations:
-delete / do not write longer paths
-combine "merged" in one vertex when further searching for a path
(This is what immediately comes to mind, maybe there are some more - then options)

Answer 3

Google's first link Is
n't it?