How to draw second order Bezier curve on GPU?

Question

GPGPU

Friends, I am faced with the task of drawing a Bezier spline consisting of a set of quadratic Bezier curves (second order, parabola) using one of the technologies / platforms that work with the GPU. Actually, the profile platform is Adobe Flash Stage3D, but the question is about the algorithm, so it's not so important. The only important thing is the absence of any ready-made solutions in the form of extensions / libraries, which, as far as I understand, take place, for example, in OpenGl.
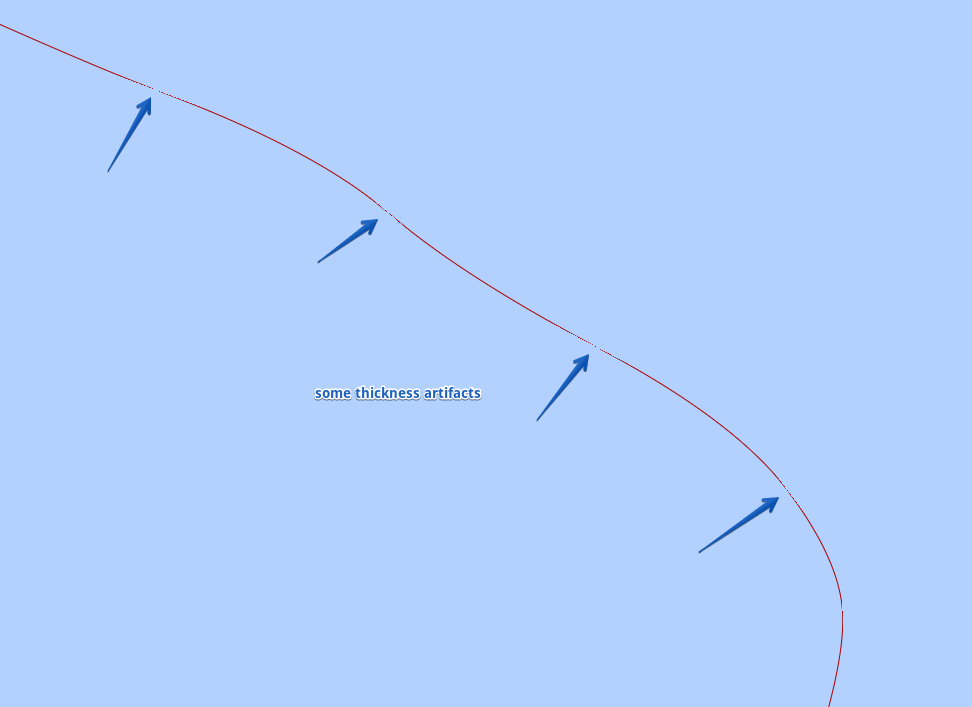
One of the important points is the fact that I would like to abandon the triangulation of a curve segment and the creation of complex geometry from many triangles for one particular segment, and get by with one (possibly several) triangles per segment. The reason why, hopefully it may be possible, is the fixed thickness of the curve segment - 1-2px, with a curve length ten times longer than that.
I am currently using the algorithm described in Loop/Blinn research.microsoft.com/pubs/78197/p1000-loop.pdf or GPUGems3 http.developer.nvidia.com/GPUGems3/gpugems3_ch25.html
Now the fragment shader looks like this:

float4 QuadraticPS(float2 p : TEXCOORD0,  
  float4 color : COLOR0) : COLOR  
{  
  // Gradients  
   float2 px = ddx(p);  
   float2 py = ddy(p);  
  // Chain rule  
   float fx = (2*p.x)*px.x - px.y;  
   float fy = (2*p.x)*py.x - py.y;  
  // Signed distance  
   float sd = (p.x*p.x - p.y)/sqrt(fx*fx + fy*fy);  
  // Linear alpha  
   float alpha = thickness - abs(sd);  
  if (alpha > 1)       // Inside  
    color.a = 1;  
  else if (alpha < 0)  // Outside  
    clip(-1);  
  else                   
  // Near boundary  
    color.a = alpha;  
    return color;  
}

which allows you to get an output like this:

As we can see - it would be great if we could get a Bezier curve segment in one triangle - but in areas close to the corners, the thickness of the line changes (since part of it seems to go into a negative area) . What, when displaying a real spline, leads to the following effect:

Please tell me how you can solve this problem and is it really possible to get by with just a few triangles (to display the "negative" sections of the curve near the corners)?
Any help is worth its weight in gold!

Answer 1

Perhaps Starling will draw better
forum.starling-framework.org/topic/graphics-class
forum.starling-framework.org/topic/drawinggraphics...