How to decompose the rotation around an arbitrary axis into rotations around the unit vectors of the SC of the object?

Question

Mathematics

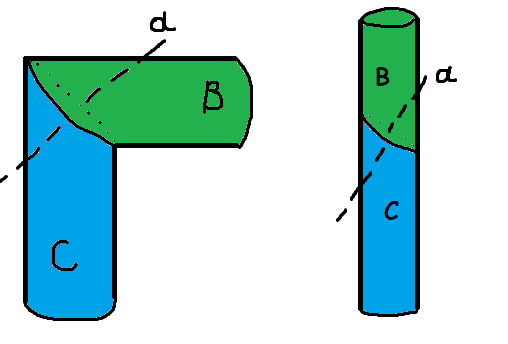
There is a swivel arm with a 45 degree swivel mount. Around the axis "a" rotates "B" relative to "C".
The image shows two extreme opposite positions. How to represent the revolution around "a" by revolutions of the SC of the green joint? Analytically, it seems that it would be correct to move from one position to another, for example, 180 degrees around the axis, perform 3 and rotate 90 degrees. However, in fact, I see how the joint draws the infinity sign. I'm looking for the ability to lay out a rotation by any number of degrees.
I found an article on the wiki about rotors, but impudently did not understand anything. Can someone on the fingers and cats explain how to twist it?

Answer 1

So. So, I twist 3 axles in turn, and not simultaneously. I'm sorry I didn't mention that in the question.
For a 45 degree angle, it's enough to rotate delta/2 along 2 axes, excluding the main axis, which you would rotate if the segments were connected perpendicularly. The answer is very simple, I mowed elsewhere.

Answer 2

180 degrees along the axis along the green detail (to the right), and then 90 degrees along the axis perpendicular to the details (axis towards us). Well, or in the reverse order - first 90 degrees along the perpendicular axis, then 180 along the longitudinal axis (up).