Answer the question
In order to leave comments, you need to log in
How to count very large numbers, and in what programming language?
Hello.
“
I beg you to take this matter seriously. I want to know the expert opinion of programmers and mathematicians. So here's the crux of the matter. There are very huge numbers in the world, and they are probably somehow counted so that you understand that there are an astronomically huge number of zeros in these numbers, not one modern calculator is able to enter at least one number, not to mention multiply, add , divide, subtract, or exponentiate the second number. In order not to spend a whole day writing just one number for an example, I am attaching
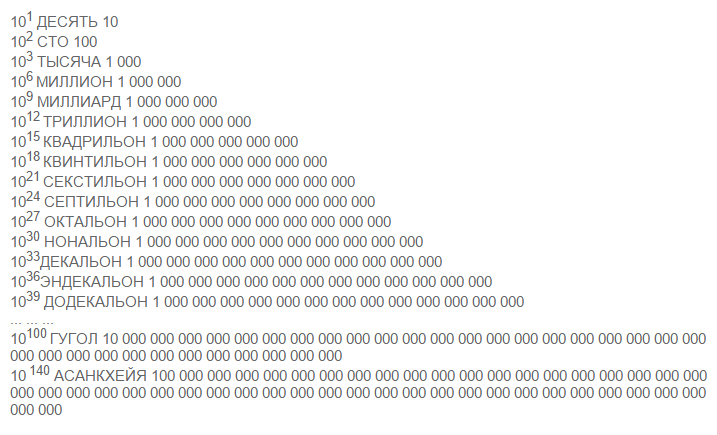
Answer the question
In order to leave comments, you need to log in
Not so big numbers :)
https://github.com/aleaxit/gmpy
In addition, look towards Fortran, there are many ready-made libraries for scientific computing.
In general, there are libraries for any PL
I do not pretend to be a solution, but I think that it is better to write the number in a String or a similar string and count it as parts
Any library with arbitrary-precission support will do.
But it seems to me that the author does not need it. Physical quantities (distances) cannot be changed so precisely that even 40 minor signs make sense.
In short, it's impossible.
In detail, they use all sorts of tricks:
1. symbolic calculations (when we simplify formulas instead of numbers)
2. relative precision (when we set unnecessary signs to zero)
So, Avogdaro's number = R / k = 6e23, and there is no huge number of digits there.
But if you want to make sure that the solution is impossible, then just go from the binary / decimal number system to, for example, bytes. Then your number can be written as a BigInt:
sign*(type_size^n*array[n]+...+type_size^1*array[1]+type_size^0*array[0])Use math packages like Maple or Matlab.
There are free alternatives.
I made an app like this a long time ago. Though, did only addition of numbers. I had to make a 64bit version in order to consider numbers "long" in more than millions of characters. Made in Delphi. The code is rather modest.
https://github.com/HemulGM/HandleSumm
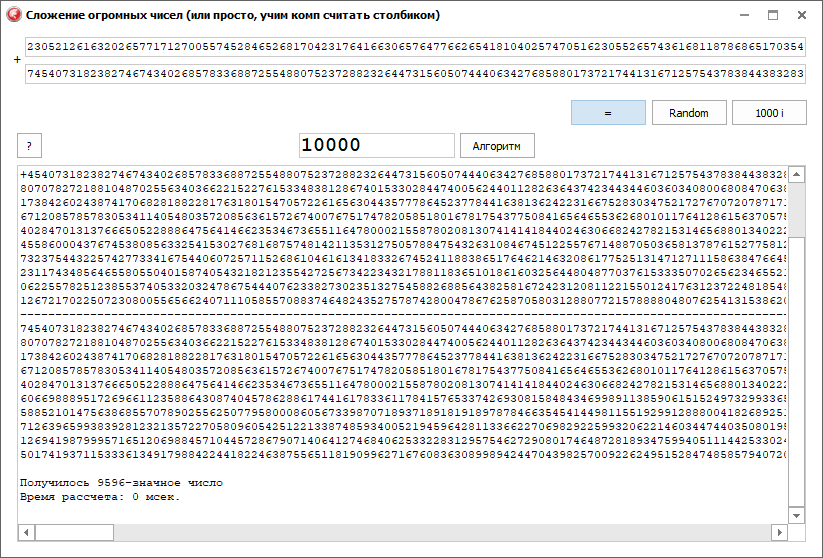
So try python: the only thing that limits it is the RAM. Almost half a million characters weighing almost four hundred MB counted in 3 seconds
import sys
X = 124456**78901
sys.getsizeof(str(X))/1024, len(str(X))
# (392.6279296875, 402002)julia> @time X = BigInt(124456)^7890123;
0.848368 seconds (6.49 k allocations: 146.362 MiB, 9.79% gc time)
julia> length(string(X))
40200302Even if you take the first of the Top-500 supercomputers and, discarding the entire computer device, you can use all of its RAM ( 250 petabytes ) to encode a single number, then the maximum will have (very rough estimate) only 6.7 * 10^17 characters. Not even close to googolplex :)
The concept of "calculation accuracy" is well illustrated by an anecdote:
Guide in the museum:
- This exhibit is about 3005 years old.
Excursionist:
- How did you define it so precisely!?
Guide:
- 5 years ago, when I got a job, the director said that this exhibit is about 3000 years old
. In real life, large exact numbers are needed only in encryption algorithms and nowhere else.
As a rule, a large number is represented as an array of bytes and there are corresponding functions for processing them. I even dabbled in it myself for a long time, there is nothing complicated there.
Your GOOGOL is only 42 bytes, and RSA algorithms use numbers 64 or more bytes long
There are also algorithms for calculating the number pi, but this is a slightly different story that has no practical use.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question