How to calculate the weight of the floor lamp base?

Question

Mathematics

Hello!
I want to make such a floor lamp with my own hands.

Tell me how to calculate the weight of the base so that it does not screw up under the weight of the weight of the arc and the lampshade?
Thank you!

Answer 1

For calculation, you can take only one axis, the second floor lamp is mirror-symmetrical and stable. We take the center of the base as 0.
1. Base - radius R _main , mass M _main
2. Vertical pipe - distance from the center of the base X _W , mass M _W
3. Arc, the most difficult part, we will take as a sector of 90 °, radius R _d , mass M _d
4. Removal - length L _in , mass M _in
5. Luminaire - mass M _sv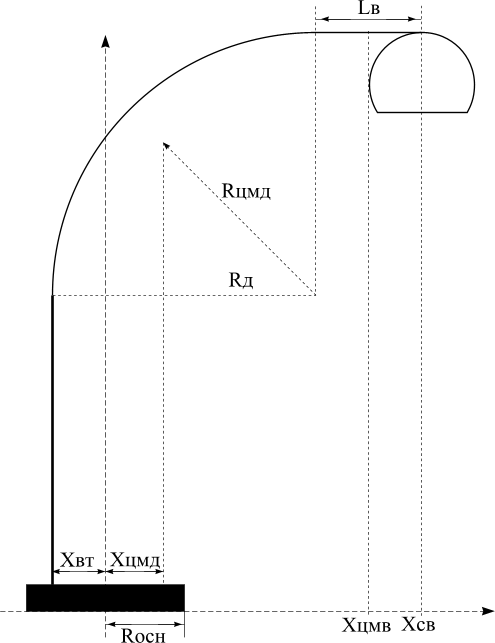
To begin with, let's calculate the location of all centers of mass.
R _cmd = R _d *sin(π/4)/(π/4) = 0.9*R _d
X _cmd = R _d- R _cmd *cos(π/4) - X _W
X _cmv = R _d - X _w + L _in / 2
X _sv = R _d - X _W + L _in
Now take the formula for the center of mass of a complex object
X _cm = SUM (X _i * M _i ) / SUM(M _i ) Impose
a constraint X _cm < R _main
(-X _w *M _w + X _cmd *M _d + X _cmv *M _w + X _sv* M _sv ) / (M _main + M _w + M _d + M _c + M _sv ) < R _main
(M _main + M _w + M _d + M _c + M _sv ) > (-X _w *M _w + X _cmd *M _d + X _cmv *M _in + X _sv *M _sv ) / R _main
M _main > (-X _w *M _w + X _cmd *M _d + X _cmv* M _in + X _sv * M _sv ) / R _main - M _w - M _d - M _in - M _sv