How to calculate the reduction factor of a square inscribed in a square at an angle of n degrees?

Question

css

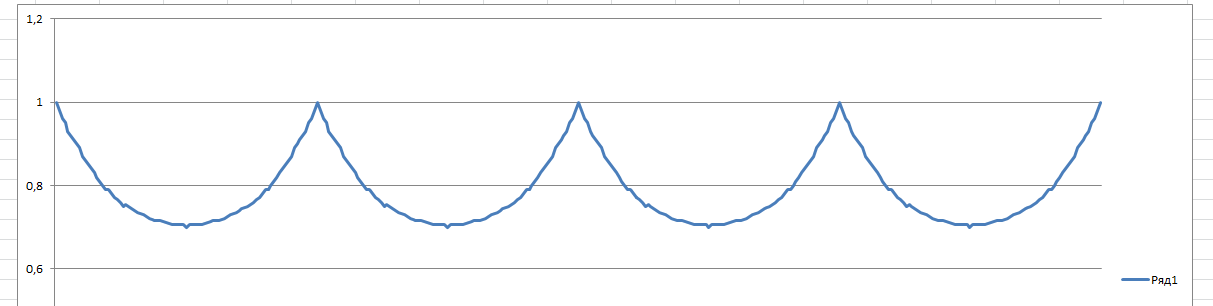
The parent container-square is located on the form. It has an inscribed element - also a square rotated by an arbitrary n-angle using CSS transform:rotate(Ndeg)where N is an angle from 0 to 360. At the same time, it is necessary that the inscribed square touches the parent container and does not go beyond its borders - for this, transform:scale(func(N))where func( N) is a function that returns the transformation ratio for a given angle. Empirically calculated the values ​​of these coefficients for angles 1,2,3 ... 45, after which they are repeated again in reverse order and so on endlessly.

Coefficient tables

const tbl={
0:1,
1:0.98,
2:0.96,
3:0.95,
4:0.93,
5:0.92,
6:0.91,
7:0.9,
8:0.89,
9:0.87,
10:0.86,
11:0.85,
12:0.84,
13:0.83,
14:0.82,
15:0.81,
16:0.8,
17:0.79,
18:0.79,
19:0.78,
20:0.77,
21:0.765,
22:0.76,
23:0.75,
24:0.755,
25:0.75,
26:0.745,
27:0.74,
28:0.735,
29:0.7325,
30:0.73,
31:0.725,
32:0.72,
33:0.7175,
34:0.715,
35:0.7155,
36:0.716,
37:0.713,
38:0.71,
39:0.7075,
40:0.705,
41:0.705,
42:0.705,
43:0.705,
44:0.705,
45:0.7,
46:0.705,
47:0.705,
48:0.705,
49:0.705,
50:0.705,
51:0.7075,
52:0.71,
53:0.7125,
54:0.715,
55:0.7155,
56:0.716,
57:0.718,
58:0.72,
59:0.725,
60:0.73,
61:0.7325,
62:0.735,
63:0.74,
64:0.745,
65:0.7475,
66:0.75,
67:0.755,
68:0.76,
69:0.765,
70:0.77,
71:0.78,
72:0.79,
73:0.79,
74:0.8,
75:0.81,
76:0.82,
77:0.83,
78:0.84,
79:0.85,
80:0.86,
81:0.87,
82:0.89,
83:0.9,
84:0.91,
85:0.92,
86:0.93,
87:0.95,
88:0.96,
89:0.98,
90:1,
}

BUT, storing an array of manually calculated coefficients (with an accuracy of 4 digits) somehow seems to me not the right way at all. There must be some formula for calculating the coefficient based on the fact that we know the angle of rotation and all the parameters of the parent container?

Answer 1

Inner side x
Outer side kx
At the same time, the outer side is the sum of the legs, i.e. xcos(a)+xsin(a) .
Then k=cos(a)+sin(a)

Answer 2

Friends! Many thanks to everyone for their active participation in solving this problem. From a geometric point of view, probably the simplest solution can be considered the option proposed by the Inventor of Dikpicks, and if we take a control angle of 45 degrees, then the coefficient will be equal to 2. BUT, at the same time, for CSS-scale, I need a value of 0.7 for 45 degrees