How to calculate the nth sum of a series?

Question

Mathematics

Problem for algorithms.
Condition: Count

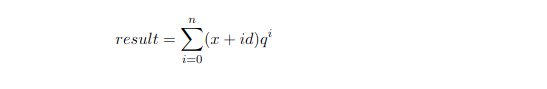
Input: x, d, q, n.
Restrictions:


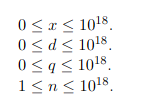
By simple summation, it gives the Timelimit. Tell me how to be

Answer 1

can be calculated analytically. I won’t deduce the formula in its entirety (it will even be written down here), but the idea is this: the
initial common term of the series a _i = x*q ⁱ + i*d*q ⁱ
the first part is an ordinary geometric progression, the second is more interesting, up to a constant : i*q ⁱ
To find the sum of such a series, you can write it like this:
q
+
q ² + q ²
+
q ³ + q ³ + q ³
+
...
+
q ⁿ + ... + q ⁿ
and sum not by rows, but by columns. Each column is a geometric progression with the sum (q ⁿ⁺¹ - q ^k )/(q - 1)
This case must be summed over k - here is a constant + a common term of a geometric progression, everything is simple. Answer: (n*q ⁿ⁺¹ - (q ⁿ⁺¹ - q)/(q-1)) / (q-1)
Then put everything together with constants into one formula.