How to calculate the combination of knight steps on a 4 by 3 matrix?

Question

Mathematics

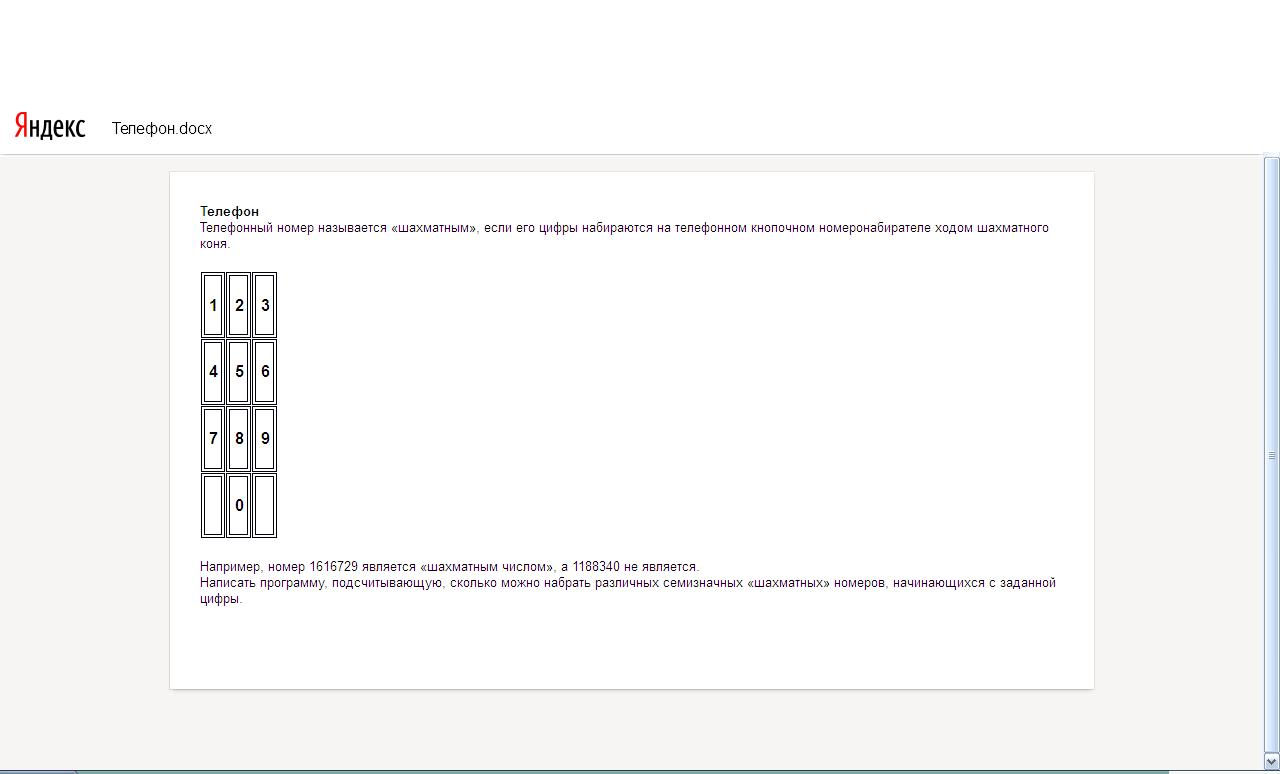
if it’s hard to see, then I
can’t calculate the chess numbers on a 4 by 3 matrix. I can’t save the place of the knight’s step and go further from this step. Do I need recursion? Then most likely a function is needed, I can not understand what arguments the function needs. If you uncomment the lines in the code, then it will show the correct valid steps at a time.

int x=0,y=0;
    for(int i=0; i<4;i++) {
        for(int j=0; j<3;j++) {
        x=i;
        y=j;
        a[3][j] = 0;
        cout<<a[i][j]<<endl;
        if (x + t < 4 && y + o < 3) { c++; x=i+t; y=j+o; printf("a[%d][%d] - %d\n", x, y, a[x][y]);  /*x=i;y=j;*/ }
        if (x + t < 4 && y - o > -1) { c++; x=i+t; y=j-o; printf("a[%d][%d] - %d\n", x, y, a[x][y]);  /*x=i;y=j;*/ }
        if (x + o < 4 && y + t < 3) { c++; x=i+o; y=j+t; printf("a[%d][%d] - %d\n", x, y, a[x][y]);  /*x=i;y=j;*/ }
        if (x + o < 4 && y - t > -1) { c++; x=i+o; y=j-t; printf("a[%d][%d] - %d\n", x, y, a[x][y]);  /*x=i;y=j;*/ }
        if (x - t > -1 && y + o < 3) { c++; x=i-t; y=j+o; printf("a[%d][%d] - %d\n", x, y, a[x][y]);  /*x=i;y=j;*/ }
        if (x - o > -1 && y + t < 3) { c++; x=i-o; y=j+t; printf("a[%d][%d] - %d\n", x, y, a[x][y]);  /*x=i;y=j;*/ }
        if (x - t > -1 && y - o > -1) { c++; x=i-t; y=j-o; printf("a[%d][%d] - %d\n", x, y, a[x][y]);  /*x=i;y=j;*/ }
        if (x - o > -1 && y - t > -1) { c++; x=i-o; y=j-t; printf("a[%d][%d] - %d\n", x, y, a[x][y]);  /*x=i;y=j;*/ }
}
}

result: (goes to minus, although the condition should not allow)

1
a[2][1] - 8
a[-2][1] - 0
2
a[2][2] - 9
a[1][-1] - 3
a[-1][3] - 1
3
a[2][1] - 8
a[-2][3] - 0
4
a[3][1] - 0
a[-1][1] - 2
5
a[3][2] - 0
a[-1][0] - 0
6
a[3][1] - 0
a[-1][3] - 1
7
a[3][2] - 0
a[0][-1] - 1
8
a[0][2] - 3
9
a[3][0] - 0
a[0][3] - 4
0
a[1][1] - 5
0
a[1][2] - 6
a[2][-1] - 6
0
a[1][1] - 5

Answer 1

Such tasks are not considered a round robin, but rather recursively. for example, we have an entry point -
we first go through all possible transitions - we get the next 2-3 digits and in fact we have 2-3 more entry points, from which we count all the next possible transitions. And so we fail until we count to the seventh point. For example: 1 -6.8; 16 - 7.1: 18 - 1.3; 167 - 2.6 etc. until we get a line of 7. To optimize, we build a two-dimensional array, one dimension of which is the numbers on the phone, and the other is an array of possible transitions

Answer 2

Incorrect approach.
You need to create the correct dictionary and then go through all the combinations in the dictionary.

Answer 3

Your job is caching overkill.
For each button, we manually throw horse “neighbors” into the array - none for 5, three for 4 and 6, two for the rest.
Then get a 10x7 array (start buttonxlength) and recurse with one small addition: if it's cached, fetch it from the cache. Rules - f(b, 1) = 1, for the rest - sum{c=neighbor(b)} f(c, i−1).
You can also use dynamic programming, without recursion - all the same, the consumption of computing power is insignificant. First f(b, 2), then f(b, 3), and so on. up to 7.

Answer 4

The question is not related to react absolutely. To send data, you need to use a POST request. Of the libraries for xhr requests, I personally like isomorphic-fetch
PS You can at least use $.ajax (from the jquery library), at least native xhr ...

Answer 5

You can use axios .

Answer 6

Use Saga