How to calculate and check equality?

Question

Mathematics

Hello!
Does anyone know how to prove that this equality (limit?) is equal only for PI?
And is this true only for PI, are there other values ​​at which equality is satisfied?
This refers to the so-called. "classical limits" or in what category can this be attributed?
What is the mathematical basis behind this?



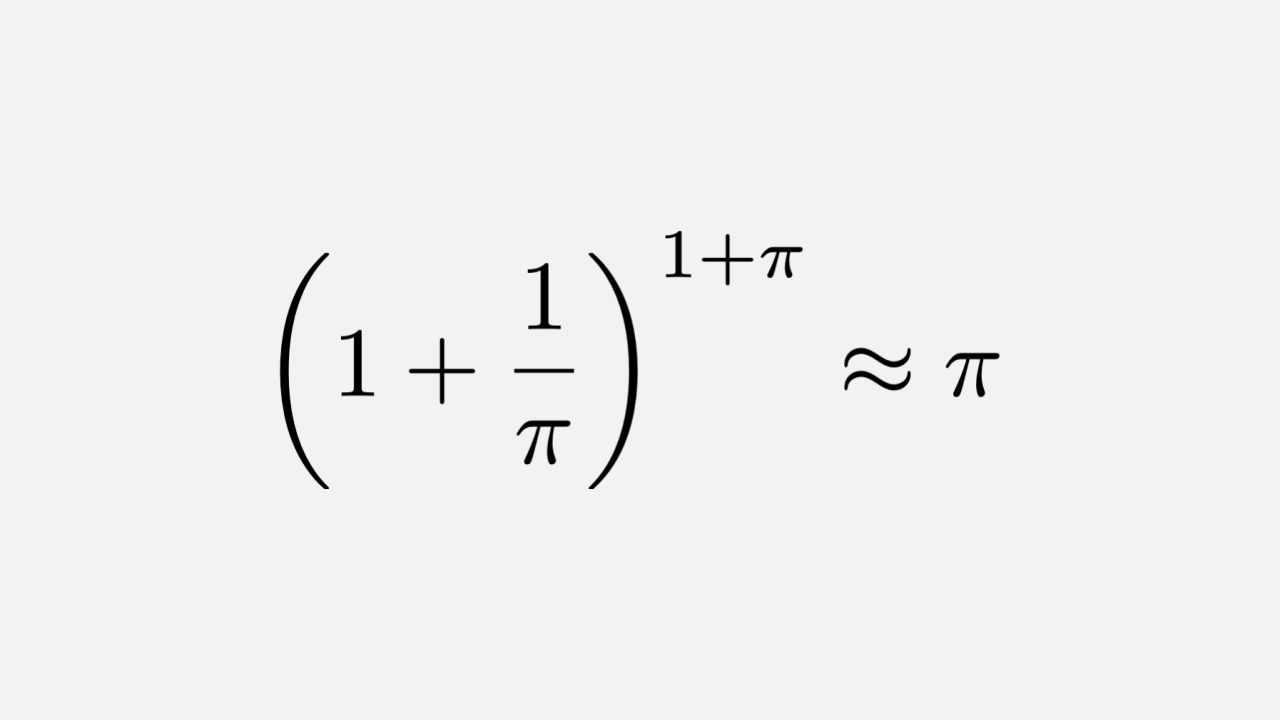
Thanks in advance for your replies!
PS I completely forgot math, the last time I did it at this level was more than 20 years ago, probably ... I don’t remember anything already

Answer 1

Take the function f(x)=(1+1/x)^(1+x)-x.
Through matan (take the derivative, make sure that it is always negative. Calculate the value of f (x) at x=1), you can make sure that the function has no roots, except for one on the segment (1, + inf), because it always decreases for units is positive.
Now we know that only one number satisfies this equation.
Apparently, the root is not pi: https://www.wolframalpha.com/input/?i=%281+%2B+1%2...
The fact that it is somewhere there can be understood if you calculate the function in points 3.1, 3.2, 3.3 - between two, where the function changes sign, and the root lies.