How many steps in finding the largest divisor in Euclid's algorithm?

Question

Algorithms

The first step of the Euclidean algorithm for given numbers m=1 and n=5 is repeated once, since the remainder of 5/1 is 0.

For m=2, this step is performed 5/2 - twice.
Well, and further:
m=3 - 3 times.
m=4 - 2 times
m=5 - 1 time.

So, we get a series of numbers 1,2,3,2,1.

However, in Knuth's answer to the question of how many times the first step of the algorithm is repeated for n=5, there is a series of numbers: 2,3,4,3,1.



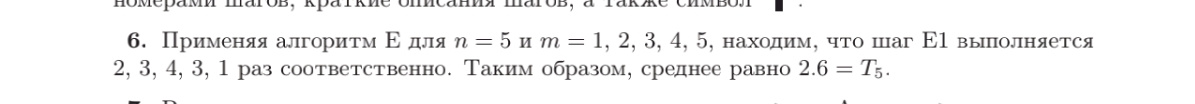
I don't know why. Who will answer?

First volume, section 1.1 task 6.

Answer 1

I understood the error. The question is not in the calculation algorithm, but in the input data.
I immediately enter the largest number into the dividend, and the smallest number into the divisor, on the machine in the implementation. That is, my first operation is not 1/5, but 5/1. Accordingly, I get 1 step less.
Now everything is all right.

Answer 2

n=5, m=1. the first step is to divide, it remains n=1, m=0. The second step is to check, notice 0 and stop.
n=5,m=3, the first step is to divide. left n=3, m=2. The second step - we divide again, it remains m=2, n=1. The third step - we divide, it remains n=1, m=0, the fourth step - we see 0, we stopped.
for n=m=5 the answer is 1, probably because the algorithm checks m==0 || m == n.