How can you calculate the area of ​​a complex figure?

Question

Algorithms

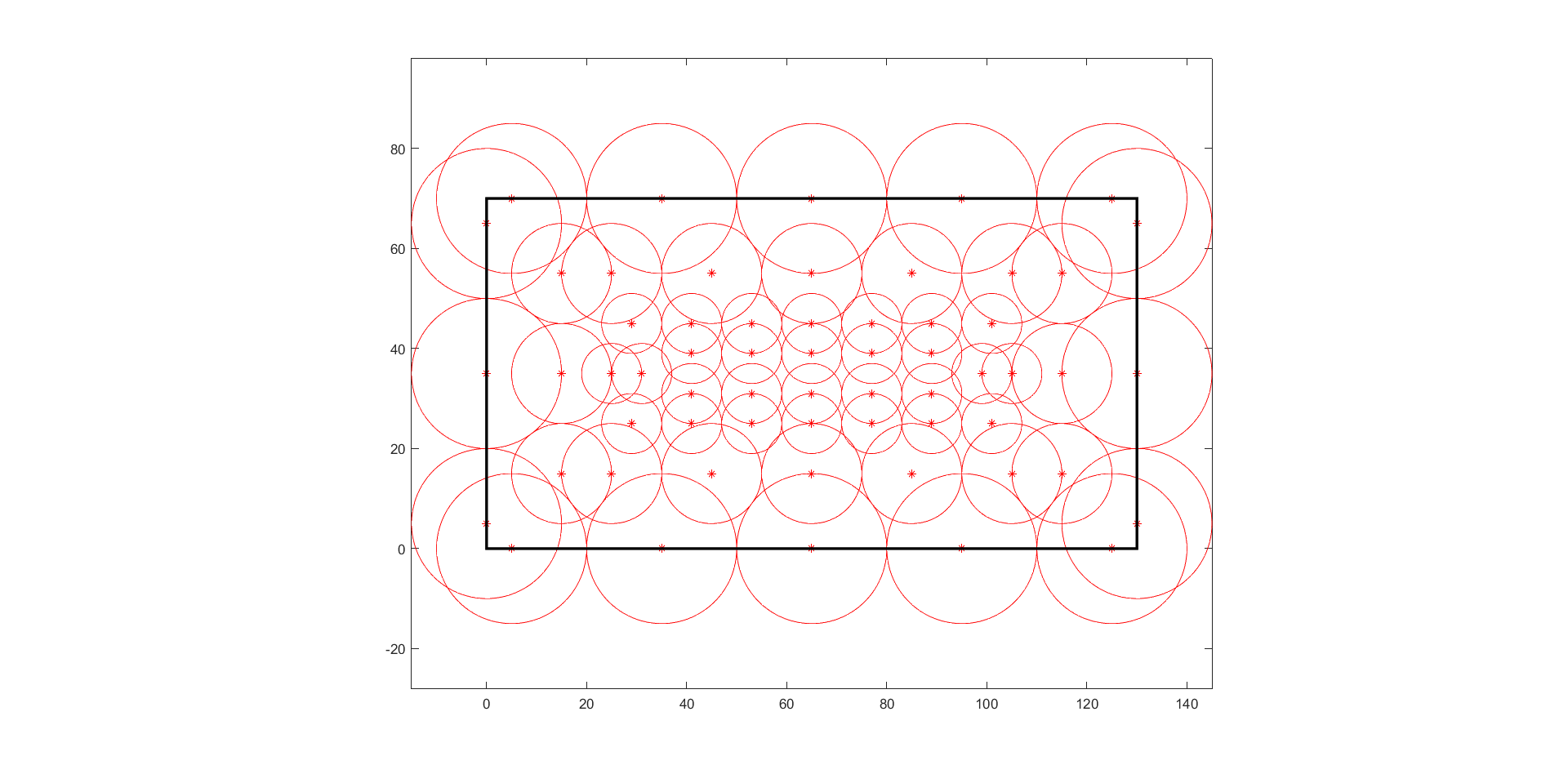
I have a program that uses points to draw circles in a given area.
It is necessary to calculate the coverage area, for this it is more optimal (most likely) to calculate the area that remains uncovered. In the figure, the result of the program

Increased the upper left corner and painted over the uncovered areas for clarity:


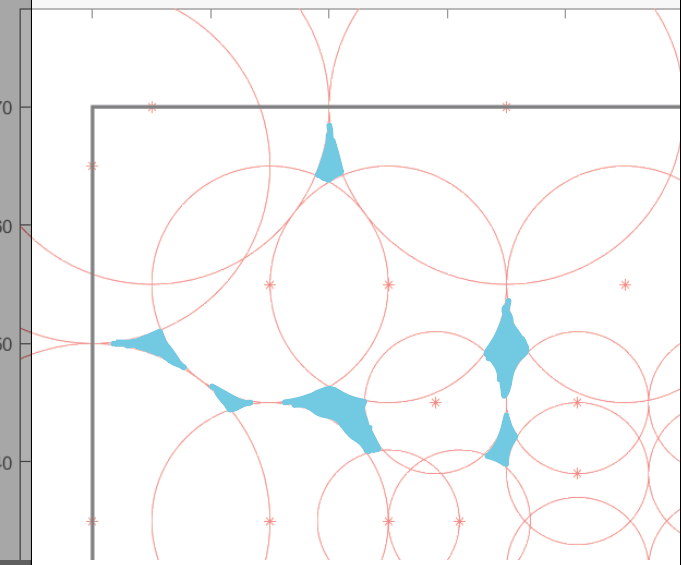
Of the circles, only their radii are known, but you can find the intersection points from the graph.

I don’t understand how you can calculate through integrals if f (x) is not set.
Just in case, I attach the construction of a circle:

R = 2;
X = 2;
Y = 2;
phi = linspace(0,2*pi);
x = X + R*cos(phi);
y = Y+ R*sin(phi);    
plot(x, y,'r', X,Y, 'r*');

Answer 1

Python Code

import numpy as np
from skimage import draw

height, width = 700, 1300
image = np.zeros((height, width), dtype=np.uint8)

# генерируем рандомные окружности
N = 250
np.random.seed(10)
xy = np.random.randint((0, 0), (height, width), (N, 2))
radii = np.random.randint(40, 60, N)


# закрашиваем окружности (цветом 1, фон 0)
for x, y, r in np.column_stack((xy, radii)):
    rr, cc = draw.disk((x, y), r, shape=(height, width))
    image[rr, cc] = 1


# подсчитываем количество ненулевых пикелей
# или просто суммируем, если единицы
# и получаем долю от всех пикселей
area_percent = np.count_nonzero(image)/(height * width)
print(f'площадь занимаемая окружностями {area_percent*100}%')

Conclusion: It is площадь занимаемая окружностями 88.35087912087913%
possible to increase the image resolution by scaling the circles and get a high area accuracy.

Answer 2

As Ilya wrote , you can rasterize the image and count the unpainted pixels. This is an easy-to-implement method, but if high precision is needed, it will be very slow and memory-intensive (exponential time and memory of the number of characters needed). However, there is an algorithm that allows you to get the area in symbolic form (of type 3/2+5113/11*sqrt(31)). Well, or any number of characters you need without huge memory consumption or calculations (the method is polynomial in the number of calculated characters).
This is some generalization of the method of selecting areas or finding the faces of a planar graph .
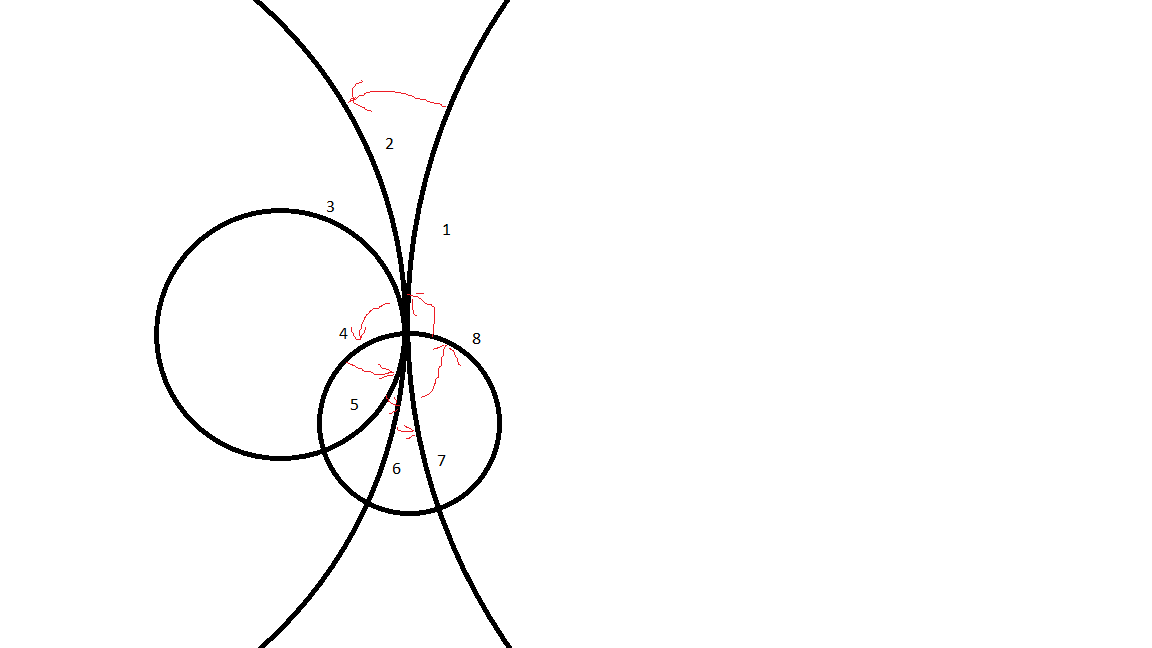
First you need to intersect all pairs of circles and circles with a rectangle, assign unique numbers to all unique points. Then you need to make a list of all intersection points on each circle and sort it along the circle (say, counterclockwise). Immediately you need to add the leftmost and rightmost point on the circle (X + -R, Y) - this will help to calculate the area later. you also need to make a list of all the points on the rectangle, also sorted counterclockwise. This list should include the vertices of the rectangle.
Now we need to build a graph: the vertices in it are the intersection points, the vertices of the rectangle, the horizontal points on the circles, and the edges are the arcs of the circles and segments of the rectangle. To do this, we sorted the points counterclockwise. Stupidly, for each circle/rectangle, we add an edge at each vertex to the next and previous vertex in the list.
Then the tricky one - you need to sort all the edges at each vertex by angle (let's say, counterclockwise again). For edges-arcs of circles, it is necessary to construct a tangent vector at a point along the arc. Then sort the arcs by these vectors (you can use the cross product of vectors). If two tangent vectors are collinear, then it is necessary to compare the radii of the circles - the larger radius lies to the right if the edges go clockwise, and to the left if the edges go counterclockwise along the circles. Those that go clockwise always lie to the right of those that go against the clock. In this case, the edges along the rectangle can be considered as circular arcs of infinite radius.
After this sorting, you have all the edges sorted by angle at each vertex. Now it is possible to find the next edge clockwise for each edge emanating from the vertex. This is the edge that will be obtained if, standing at the intersection point, go not along this edge, but along the one that goes a little to the left:

here is a picture of mad paint skillz

Also, if not obvious, graph-oriented. And during construction, you need to remember the opposite for each edge.
Now you can select all areas in the figure: you need to, as in the algorithm from the link above, take any edge that has not yet been processed and in a loop, until you return to it, go to the back edge and from it to the next corner from the vertex. In this way, the area is simulated by turning as far to the left as possible. Or as if you are on a plane inside the area and go around it with your right hand against the wall.
As a result, each closed area will be bypassed counterclockwise. Except for one exception - the whole picture will be traversed along the border in a clockwise direction, but this can be easily checked through the vector products of adjacent arcs (tangents) and throw this area out of consideration. You will have a list of rectangle arcs/segments. Now it remains to understand which areas are not covered by circles. First, if the area has a convex arc (counterclockwise arc along the circle), then the area is 100% inside the circle. Secondly, we need to take any vertex of the region and check whether it lies strictly inside any circle.
If the area was not covered, then you can take its area and add it to the answer. Here it helps us that we put horizontal points on the circle - all the edges of the area are either strictly vertical segments or go horizontally, like a graph of a function. This means that you can take the integral over x (you know which circle the edge belongs to, you know the boundaries for x and the upper or lower bound of this).
This is how the answer is. All coordinates can be read in symbolic form - they will be of the form a/b+sqrt(c)/d. The tangent vectors will be of the same type. Such numbers can be multiplied, added, subtracted and compared. True, after operations you will get a lot of radicals, but there is no problem, because you no longer have to compare the results. Well, or here you can use floating point numbers and calmly get 12-14 digits of precision.