How are two types of derivative obtained, using the example of a sigmoid?

Question

Mathematics

Let's find the derivative of the function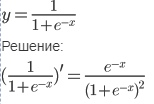

f(x) = 1 / (1 + e^(-x))
and I saw that its derivative is
dy/dx = f(x)' = f(x) * (1 - f(x))
The derivative is considered so in machine learning
Where to study this topic in detail, help to understand the second kind of derivative.
Thank you!

Answer 1

The derivative of the quotient is equal to the difference between the product of the derivative of the numerator and the denominator and the product of the numerator and the derivative of the denominator, divided by the square of the denominator.
(1/(1 + e^-x))'
= (1' * (1 + e^-x) - 1 * (1 + e^-x)')/(1 + e^-x)^2 #according to the formula for the derivative of the quotient
=( 0 * (...) - 1' + (e^-x)' )/(1 + e^-x)^2 #according to the formula for the derivative of the sum
= (- e^-x * (-x)')/(1 + e^-x)^2 #according to the formula of the derivative of the exponent
= (e^-x)/(1 + e^-x)^2
Then
f(x) = 1/(1 + e^-x)
(e^-x)/(1 + e^-x)^2
= (e^-x)/(1 + e^-x) * 1/(1 + e^-x)
= (e^-x)/(1 + e^-x) * f(x)
= (-1 + 1 + e^-x) / (1 + e^-x) * f(x)
= (- 1 + (1 + e^-x)) / (1 + e^-x) * f(x)
= ((-1 / (1 + e^-x) + (1 + e^-x)/(1 + e^-x)) * f(x)
= (1 - (1/(1 + e^ -x))) * f(x)
= (1 - f(x)) * f(x)
That is, it's not "another way to calculate the derivative in ML", it's just transformations of the derivative of this particular function
. in mathematics for grades 8-11.