Given the set of perimeter points of a figure, how to find its area?

F

Filipp422022-01-08 00:28:19

Mathematics

Filipp42, 2022-01-08 00:28:19

Hello.
I needed a planimeter, and buying a toad is suffocating. Much more interesting to do it yourself. I decided to do this: the mechanical part consists of two movably connected rails. The rail AB rotates around a fixed point A, we can measure its angle of rotation. The slats are connected at point B, we can also measure the angle between them. At point C, a needle is fixed, which we draw along the surface of the figure. Knowing the angles and lengths of the rails, you can easily calculate the coordinates of point C at any time.

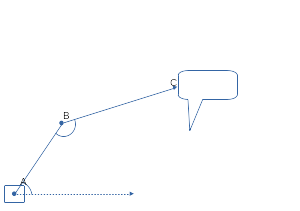
We draw along the perimeter of the entire figure and read the C coordinates once every dt. As a result, we get an array of point coordinates. Neighboring points are considered connected. The same applies to the two extremes. Please tell me how can we calculate the area of a figure? It is desirable if you do not just dump it on me, but gradually push it towards a decision.
Thank you!

Reply

Answer the question

In order to leave comments, you need to log in

4 answer(s)

R

Rsa97, 2022-01-08
@Rsa97

The area bounded by a closed contour is calculated as an integral over the contour.

V

Viktor, 2022-01-08
@nehrung

First you need to connect (you can mentally, if you have a good geometric imagination, but you can also on the drawing) the points of the vertices with straight lines so that the whole figure is divided into triangles. And for the area of a triangle there is a ready-made formula, here it is.
If the coordinates of the triangle vertices are:
A (x1; y1)
B (x2; y2)
C (x3; y3)
Then its area is
S = ½*((x2-x1)*(y3-y1) - (y2-y1)* (x3-x1))
Then we sum up the areas of all triangles and get the required area of the figure.
Found here.

M

mlyamasov, 2022-01-08
@mlyamasov

So: https://habr.com/en/post/579364/#comment_23512988

A

alekseiami, 2022-02-09
@alekseiami

Why do you need two hinges, at points A and B?
What if we just made a rigid AB rail on which the needle holder would slide?
In order to point the needle at any point on your plane, you change the angle of rotation of the rail and the distance from point A to the needle. Computing coordinates is a classic direct geodetic problem.