Generation of all possible options for filling a square matrix with the N-th number of graphs. Algorithm..?

Question

Algorithms

Hello.
There was a need to generate a complete selection of possible options for "filling" the matrix with graphs.
Or rather, their binding in various sequences. Graphs are directed chains.
That is, you need to find all possible options for chains of elements, provided that the graphs:
a) can be an arbitrary number.
b) the "length" of the chain of elements can vary.
c) a matrix of arbitrary size, but always square.
d) you can connect only standing "adjacent elements" in x or y, no diagonals.
I ask for help in finding the optimal algorithm, or at least a working one, for which it is possible to prove that the resulting sample will be complete.
UPD: I'll reformulate a little: you need to find all options for linking elements into chains. (at least 2 elements each in order to reduce the number of options)
For 2x2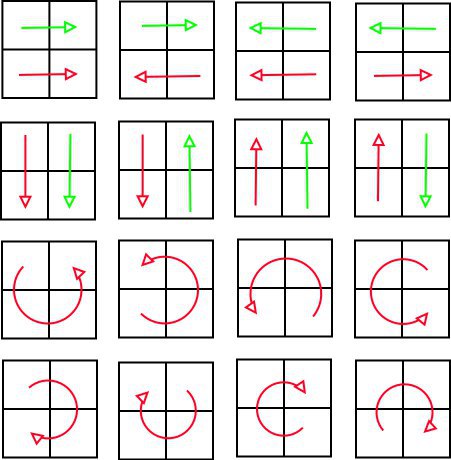

Accordingly, for 3x3 and more, the difference will be that the chains can be complex shapes and different lengths. And different quantities, in each version.

Answer 1

If we take any chain that passes through all points (for example, a snake or a spiral), and cut it into pieces in all possible ways, and then unfold some of the pieces, we will already have about 2 ^ (N ^ 2) / 3 options . Even with N=7, it is unrealistic to list them (with N=6 there are only 10 billion of them - this is not so much). But since there are many initial chains (passing through all points), and besides, not all configurations can be obtained by cutting one chain, there will be even more options.
Algorithms - both recursion and enumeration of cell states - are not very complex. In both cases, you need to look for a partition into undirected chains, and then set their direction by all means.
In the case of enumeration of states (it is simpler), we do this. Note that each cell has 10 possible states - 4 for the end of the chain (the direction the chain goes from that cell), 4 for the cell where the chain turns, and 2 for the cell it goes straight through. In addition, there are restrictions: the chain cannot rest against the wall, and the common edge of two neighboring cells is either intersected by the chain on each side or not. Well, there should be no cycles.
The algorithm turns out like this. Iterate over the matrix cells row by row. For each next cell, look at the state of its neighbors, and get a list of possible states of the cell itself - there are no more than three of them. If there is a state that connects two adjacent chains, you need to go through them - check if they are the ends of the same chain (if yes, you get a cycle, and it is forbidden). Now we substitute into the cell in turn all the admissible states, and recursively call the enumeration function for the next cell. When we reach the end, we fix the found partition.