Function for calculating the angle of rotation in a three-dimensional plane?

Question

Mathematics

Since in the ranks of programmers there are often people who know mathematics well, I would venture to ask on Habré.
I ask you not to kick too much, in geometric terminology I am a seventh grader.
There is a three-dimensional space, coordinate axes X, Y, Z (according to Descartes, if I'm not mistaken). There is a cube that stands on its bottom face.

I rotate it by a random angle along two axes (in my case, these are X and Y, the rotation angles are all different, within 0-90 degrees).

The question arose - by what formula to calculate new rotation angles in order to simply turn the cube over to another face? (need to rotate to different faces)

In my head, such an algorithm is “rotate, reset the coordinate axes to their original position, without touching the cube, rotate again”, but in practice I cannot display it. Tried to tritely sum up the rotation along each axis, multiply by the relationship between them, but the "poke" method did not help.
Thanks in advance for your help.

Answer 1

Quote from Wikipedia. Rotation matrix .
Let the axis of rotation be given by a unit vector , and the angle of rotation 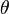. Then the rotation matrix in Cartesian coordinates looks like:

Multiplying the coordinates of some vector by the rotation matrix, you get the coordinates of the rotated vector. All sides of a cube are vectors.

Answer 2

Read: habrahabr.ru/post/131931/
There is a lot of everything on this topic from the very beginning to the matrices.
More about quaternions here or here

Answer 3

Here is a detailed manual on object rotation, matrices, Euler angles and quaternions.

Answer 4

en.wikipedia.org/wiki/Quaternions_and_rotation_of_space
I think this is it ))