Answer the question
In order to leave comments, you need to log in
Finding rotated objects?
Actually there is an image (already processed, the Canny filter is applied). It depicts the contours of a figure. The figure must always stand vertically (for further processing). The outline of the entire figure fits into a rectangle. At the moment, the problem is solved as follows. Extreme vertical/horizontal points are found, lines are drawn. The line with the maximum length is selected, the angle between the perpendicular is calculated. The image is rotated. The result is correct only in 50% of cases, since due to the rotation of the object, these “vertices” are located with a rather large error.
The objects are pear-shaped contours.
As an option, try the selection method, rotate by a certain angle, look at the dimensions of the rectangle (height) into which the contour fits, if this size is larger, rotate even until the height begins to vary within one pixel. The angle is usually not large, up to 15 degrees, but in fact this method turns out to be quite voracious. Are there any algorithms for similar tasks?
In the final etoge I have to get the coordinates of the points of the rectangle and the angle of rotation.
Image example: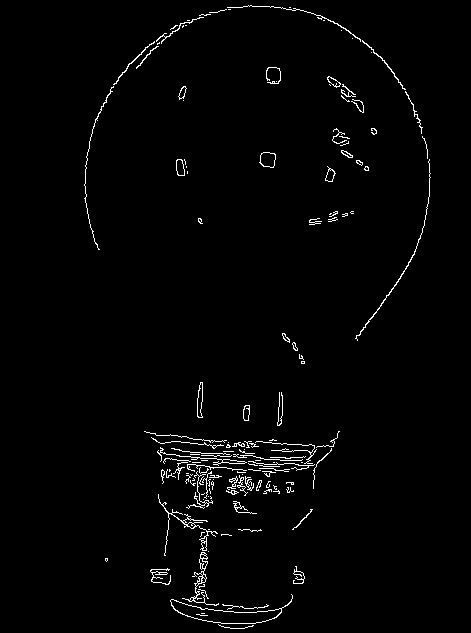
Answer the question
In order to leave comments, you need to log in
I did something like this (through python binding to OpenCV):
def how_to_make_horizontal(contour):
""" Returns rotate center and angle that would make contour horizontal """
rect = cv.BoundingRect(contour)
box = cv.MinAreaRect2(contour)
x, y, w, h = rect
p1, p2, angle = box
if angle > 45:
angle -= 90
if angle < -45:
angle += 90
rotate_center = x+w/2, y+h/2
return angle, rotate_center
And it is possible at least one example of objects? It's better to see once.
I would look for the axis of symmetry. But so far, I don't really know how. For example, take all pairs of points, build their perpendicular bisector, and calculate the statistics of their parameters in the space of lines (angle, distance from the center). It is possible that the maximum will give the right direction.
No, the center of mass (xc,yc) is taken there, then the coefficients a11=sum(xi-xc)^2, a12=a21=sum((xi-xc)*(yi-yc)), a22=sum(( yi-yc)^2), where (xi,yi) are the coordinates of all points. Next, from the matrix ((a11 a12) (a21 a22)) you need to take the eigenvectors - they will give the orientation of the object. Or they won't give it... To somehow separate the internal points from the external ones... You have to experiment a lot, the task is not easy and very heuristic.
I would try this: Taking the boundary area (where there are pixels of different colors) you can find the direction of the gradient / fill. An illustration to make it clearer: habrastorage.org/storage2/e77/b42/392/e77b42392bce4c4b73b70e4ec8c4057f.png
Armed with this knowledge, you can analyze all the boundary areas, and the sum of the directions found will be (theoretically) the desired angle of rotation. In your case, one pass of the pixel shader will be enough for this. However, please note that due to the binary format of your samples, there will be significant errors.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question