Does a random number generator SOMETIMES (very rarely!) return NaN?

Question

Fortran

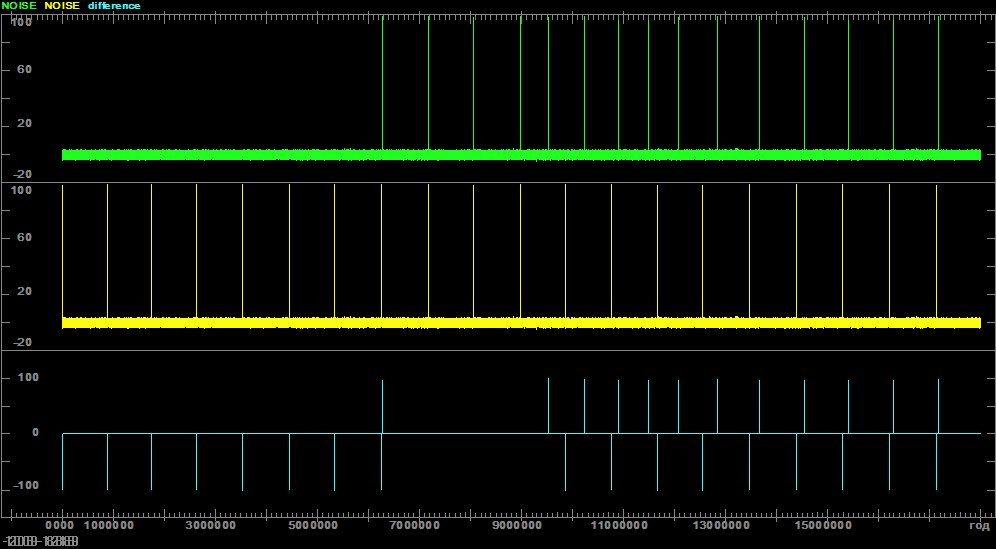
I'm doing scientific calculations, and suddenly I discovered a very strange effect. If you call the Intel (integrated in Intel Fortran) generator of uniformly distributed random numbers (0.1) many times in a row, then on some computers (so far there are 4 out of 5 tested) after about A = 50 million calls (the exact figure varies, see more details). see the link below) it starts quasi-periodically, with a period of about B=10 million calls, to return NaN.

UPD : Thanks to Tony 's leading question , I want to clarify one important nuance: even when generating the same PSN sequences (SEED initialization with the same constant), NANs appear in different places every time they start.

UPD: here are the details (picture with test results)

На этой картинке три ряда.
Первый и второй ряды (зеленый и желтый) - две это последовательности нормально распределенных ПСЧ, полученные при двух запусках тестовой программы с одинаковым SEED(301). Каждое значение сигнала на графике - это сумма 12-ти значений RANDOM минус 6. Тем самым я получаю нормально распределенное случайное число, а заодно уменьшаю длину ряда в 12 раз. Если хотя бы один из 12-ти вызовов RANDOM вернул NaN, то и значение Noise на графике тоже будет NaN. Таким образом, чтобы получить 1 000 000 значений Noise, я вызываю функцию RANDOM 12 млн раз.
Третий ряд (синий) - это разность между первым и вторым рядом.
NaN-ы, как и на всех остальных картинках, закодированы числом 99. Соответственно, разность двух первых рядов дает либо 0 (если значения совпадают), либо +-99 (примерно).



Из картинки хорошо видно, что:
1) при первом запуске теста первый NaN появляется примерно после 6.2 млн вызовов функции Noise (75 млн вызовов RANDOM). После этого NaN-ы появляются примерно через 10 млн вызовов RANDOM. Но иногда (не очень часто) этот интервал может быть существенно меньше. Например, на отметках 9 и 9.5 млн.

2) А вот при втором запуске теста первый NaN появляется почти сразу же! "Мертвый период" (без NaN-ов) исчезающе мал. В исходном посте я писал, что этот "мертвый период" чаще всего близок к 60 млн вызовов, и лишь иногда он бывает существенно меньше. Но тогда я гонял тесты, инициализируя ГСЧ комбинацией даты и времени. А вот когда я стал подсовывать в seed небольшие натуральные числа (пробовал от 20 до 400), то оказалось, что при такой инициализации цикл с квазипериодическим появлением NaN может запускаться почти сразу же после старта программы!

3) Теперь смотрим на ряд разности (синий). Видно, что он почти везде равен нулю, т.е. последовательности ПСЧ действительно одинаковые.
За исключением NaN-ов...

4) Еще интересен фрагмент от 6.3 до 9.5 млн. На этом участке NaN-ы в двух последовательностях в точности совпадают! Напомню, что между последовательными NaN-ами примерно по 0.8 млн вызовов Noise, или около 10 млн вызовов RANDOM. То есть, вероятность случайного совпадения двух NaN-ов в рядах Noise примерно E-6. А в приведенном примере они совпали трижды подряд! Ясно, что случайностью это быть не может.

5) Однако, после совпадения трех NaN-ов подряд следующие NaN-ы (на отметке 9 500 000) в двух тестах разные! И дальше последовательности расходятся.

Из анализа этой и других подобных картинок я могу сделать такие выводы:
1) Момент появления первого NaN в последовательности как-то зависит от того, чем инициализирован генератор случайных чисел.
2) Появление NaN зависит как от внутренних переменных генератора случайных чисел (иначе мы бы никогда не увидели точное совпадение NaN в двух разных последовательностях), так и еще от каких-то внешних по отношению к ГСЧ факторов (иначе бы при одинаковом внутреннем состоянии ГСЧ NaN всегда появлялись бы в одинаковые моменты времени).

Whether a similar effect will be observed in other languages ​​/ compilers, I cannot check - I do not have a compiler / skill. But I suspect that Fortran and C often share the same basic math libraries. Even the name of the function - RANDOM in modern Fortran and C is the same. And other languages ​​can carry something from C libraries.

So far, I have made a backup for myself: I wrapped the built-in random number generator in my own function, which, in the case of isNan (Random), calls the generator again. But the inner discomfort remained. And I still want to understand the cause of the bug, and at the same time warn other "interested parties" about it.

And one more important nuance. The bug occurs only if you build a program with full optimization. In my Fortran, these are the keys /MP /O2 /QaxSSE3 /QxSSE3 /Qparallel. When building without optimization, the result will be NaN-free.
This, to put it mildly, surprised me, since the random number generator, in theory, should be called the same in both cases. Since the source code for the RANDOM function is not included with my compiler - it probably clings from some standard library - I got into the disassembler to understand the difference between the two versions of the random number generator (assembly with and without optimization). The generator itself, as one would expect, is indeed the same in both cases. But inside the RANDOM code there is

one external call

Для начала предупреждаю, что в ассемблере я ни бум-бум, и пишу только на фортране! Поэтому все написанное под этим спойлером может оказаться полным бредом и воспаленным воображением. Я всего лишь хотел попытаться, насколько сумею, собрать хоть какую-то информацию про обнаруженный баг для тех, кто проявит интерес к ситуации, но не имеет возможности открыть интел-фортран и проделать все это лично.

Итак, я дизассемблировал две версии своей тестовой программы: с ключом оптимизации /Od (оптимизация запрещена) и /O2 (оптимизация скорости). Оказалась, что сама функция-генератор случайных чисел в двух версиях идентична (с точностью до ее расположения в памяти, но это понятно).
Однако, внутри этой функции есть один внешний вызов:

005C052B call _for__acquire_semaphore_threaded (596C80h)

Внутри которого (после череды других call) происходит что-то уже совсем-совсем для меня непонятное:

75C34043 call 75C443C5
(...)
75C443C5 jmp dword ptr ds:[75BA007Ch]

Для непосвященного это напоминает call по адресу, хранящемуся в ячейке памяти (указатель на функцию?). Как такое дебажить, особенно если нештатное срабатывание может первый раз произойти через 50 млн вызовов, я себе представляю плохо. Точнее, не представляю вообще: это вопрос совершенно не моего уровня компетенций :-((

Но на всякий случай добавлю, что программа у меня однопоточная и, по идее, ничего согласовывать с другими потоками не должна. С другой стороны, в языке есть массивные операции, которые могут распараллеливаться автоматически, и, теоретически, генератор случайных чисел может в этом случае как-то донастраиваться для параллельных вычислений. В справке я об этом ничего не нашел, но это может быть не проблемой справки, а моей личной проблемой (справка написана по-английски, а у меня отношения с ним не сложились :-(.

Более полная информация, включая ассемблерный код в двух вариантах, собрана вот тут:
FORTRAN_URAND_BUG.doc
Это Word-файл, в который я собираю всю информацию про этот баг. Там же приведен исходный фортрановский код, а также дана ссылка на скачивание моего exe-шника с тестом. Если будет не влом - запустите его и напишите мне, что получилось. Пока из 5 протестированных компов Nan-ы появляются на 4-х, а на одном - нет. (Подробнее в том же Word-файле)

And another version

Глядя на битовые маски:

Random= 11111111110000000000000000000000 NaN
R=1.00 = 00111111100000000000000000000000 1.00000

возникает подозрение, что проблема может возникать на этапе преобразования int -->> real. Насколько я понимаю, исходный алгоритм генератора псевдослучайных чисел обычно работает с integer. Более того, он никогда не дает числа вида 00000000 или FFFFFFFF. Поэтому на выходе фортран-генератора не должно быть ни точных 0, ни точных 1.000. Но как известно, точность представления чисел с плавающей запятой в компе ограничена. Около 0 это не влияет, а вот вблизи 1 некоторые integer-ы могут преобразовываться в R=1.000
С другой стороны, если бы это было именно так, то код этого преобразования работал бы одинаково с оптимизацией и без нее (или нет?).
В общем, если вы заинтересуетесь и попробуете вызвать RANDOM из Си, то включайте максимальную оптимизацию. У меня бажит только оптимизированная программа. Правда, я не очень понимаю, можно ли включить в Си многопоточность одним ключом /MP, или надо специально цеплять для этого всякие либы. В фортране-то параллельность заложена в языке (массивные операторы) и от пользователя не требуется большого ума, чтобы ее подключить...

И еще для справки: вот что написано про ключ /О2 в справке фортрана:
UPD: к сожалению, я столкнулся с ограничением на длину вопроса и эту информацию вынужден отсюда убрать. Она теперь лежит все в том же злосчастном Word-файле, который доступен про ссылке.

In general, the story is already getting very long, and it gradually acquires details. You can't fit in one question - you need to write a whole article here ... But is it appropriate to do this, having only a question without an answer?

Therefore, for those to whom the question is really relevant, I am attaching a link to a Word file that contains ALL the details of the situation that I have been able to dig up so far: FORTRAN_URAND_BUG.doc .

I also wrote some details here in this comment.
It's less complete than the Word file, but it's easier to see - no need to download anything.

If you don't mind writing your own RANDOM tests, it would be very interesting to know the results. Just do not forget about optimization - without it there will be no glitches (but this is not accurate ;-)

Answer 1

I read the thread and I can make an input: either magic happens, that is, we attribute everything to magnetic storms on Jupiter, or we still need to dig.
If the bug reproduces absolutely chaotically, then I can assume (from my C ++ experience) that someone somewhere spoils the heap and you end up with garbage.
By the way, I understand that Rand in Fortran produces a number of type float / double because I do not understand how NaN is possible in integers.
Question: if you write a simple naked program in which there will be only one call to the main function (well, or whatever in Fortran, I'm sorry, I don't know) and only in this function in the loop call Rand and nothing else.
NaN - appears???
PS can you attach an asm listing of the Rand function?