Distance from a point in space to a point on the surface of a sphere?

Question

Geometry

It is necessary to achieve the following result, as shown in the figure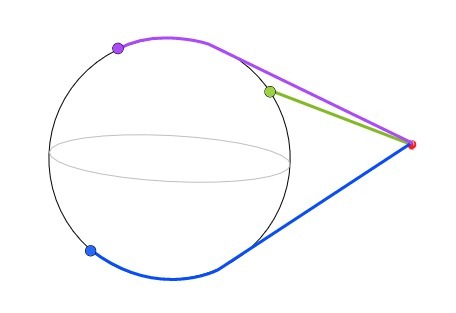

. The coordinates of the red dot and the coordinates (latitude / longitude) on the sphere are known (from can be converted to world (3D)
If you draw a straight line to the desired point, then if it is on the other side of the sphere, the line will intersect sphere. Of course, it would be possible to convert the first intersection point into sphere coordinates and already find the distance by latitude / longitude and add it to the distance to the first point, but this way the distance will be exaggerated if the point is exactly on the opposite side.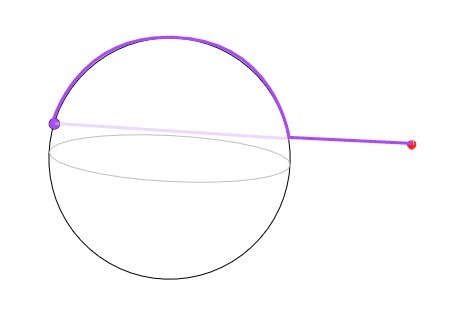

UPD: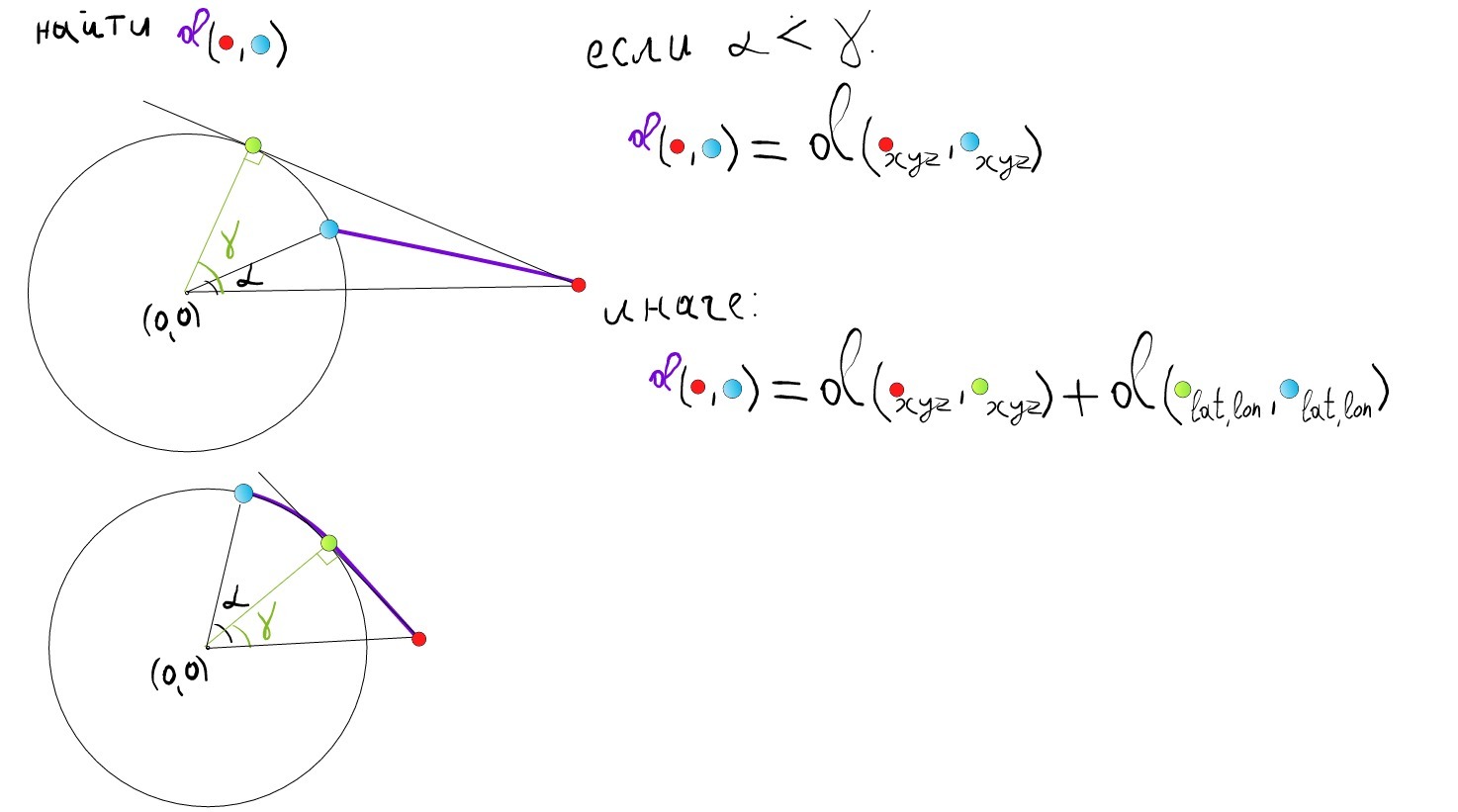

it remains to figure out how find the tangent point to the sphere

Answer 1

1. We set a single reference point (if it does not exist).
2. Through the latitude / longitude and the radius of the sphere, we determine (x1,y1,z1) points on the sphere.
3. We bring a point in space to a reference point. We get (x2,y2,z2).
4. Through several quadratic equations we find the distance. It is possible through the service , there is a formula.