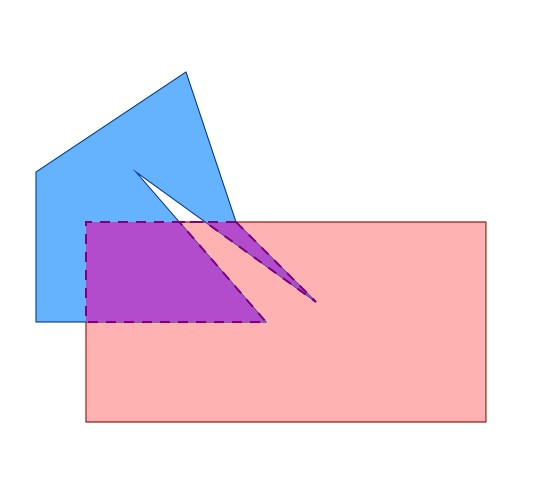
Cropping a non-convex polygon. How to determine the set of polygons in the output?

Question

C++ / C#

Hello. Here https://rosettacode.org/wiki/Sutherland-Hodgman_po... is a program for cutting a polygon (subject) with a rectangle (clipper).

code

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
 
typedef struct { double x, y; } vec_t, *vec;
 
inline double dot(vec a, vec b)
{
  return a->x * b->x + a->y * b->y;
}
 
inline double cross(vec a, vec b)
{
  return a->x * b->y - a->y * b->x;
}
 
inline vec vsub(vec a, vec b, vec res)
{
  res->x = a->x - b->x;
  res->y = a->y - b->y;
  return res;
}
 
/* tells if vec c lies on the left side of directed edge a->b
 * 1 if left, -1 if right, 0 if colinear
 */
int left_of(vec a, vec b, vec c)
{
  vec_t tmp1, tmp2;
  double x;
  vsub(b, a, &tmp1);
  vsub(c, b, &tmp2);
  x = cross(&tmp1, &tmp2);
  return x < 0 ? -1 : x > 0;
}
 
int line_sect(vec x0, vec x1, vec y0, vec y1, vec res)
{
  vec_t dx, dy, d;
  vsub(x1, x0, &dx);
  vsub(y1, y0, &dy);
  vsub(x0, y0, &d);
  /* x0 + a dx = y0 + b dy ->
     x0 X dx = y0 X dx + b dy X dx ->
     b = (x0 - y0) X dx / (dy X dx) */
  double dyx = cross(&dy, &dx);
  if (!dyx) return 0;
  dyx = cross(&d, &dx) / dyx;
  if (dyx <= 0 || dyx >= 1) return 0;
 
  res->x = y0->x + dyx * dy.x;
  res->y = y0->y + dyx * dy.y;
  return 1;
}
 
/* === polygon stuff === */
typedef struct { int len, alloc; vec v; } poly_t, *poly;
 
poly poly_new()
{
  return (poly)calloc(1, sizeof(poly_t));
}
 
void poly_free(poly p)
{
  free(p->v);
  free(p);
}
 
void poly_append(poly p, vec v)
{
  if (p->len >= p->alloc) {
    p->alloc *= 2;
    if (!p->alloc) p->alloc = 4;
    p->v = (vec)realloc(p->v, sizeof(vec_t) * p->alloc);
  }
  p->v[p->len++] = *v;
}
 
/* this works only if all of the following are true:
 *   1. poly has no colinear edges;
 *   2. poly has no duplicate vertices;
 *   3. poly has at least three vertices;
 *   4. poly is convex (implying 3).
*/
int poly_winding(poly p)
{
  return left_of(p->v, p->v + 1, p->v + 2);
}
 
void poly_edge_clip(poly sub, vec x0, vec x1, int left, poly res)
{
  int i, side0, side1;
  vec_t tmp;
  vec v0 = sub->v + sub->len - 1, v1;
  res->len = 0;
 
  side0 = left_of(x0, x1, v0);
  if (side0 != -left) poly_append(res, v0);
 
  for (i = 0; i < sub->len; i++) {
    v1 = sub->v + i;
    side1 = left_of(x0, x1, v1);
    if (side0 + side1 == 0 && side0)
      /* last point and current straddle the edge */
      if (line_sect(x0, x1, v0, v1, &tmp))
        poly_append(res, &tmp);
    if (i == sub->len - 1) break;
    if (side1 != -left) poly_append(res, v1);
    v0 = v1;
    side0 = side1;
  }
}
 
poly poly_clip(poly sub, poly clip)
{
  int i;
  poly p1 = poly_new(), p2 = poly_new(), tmp;
 
  int dir = poly_winding(clip);
  poly_edge_clip(sub, clip->v + clip->len - 1, clip->v, dir, p2);
  for (i = 0; i < clip->len - 1; i++) {
    tmp = p2; p2 = p1; p1 = tmp;
    if(p1->len == 0) {
      p2->len = 0;
      break;
    }
    poly_edge_clip(p1, clip->v + i, clip->v + i + 1, dir, p2);
  }
 
  poly_free(p1);
  return p2;
}
 
int main()
{
  int i;
  vec_t c[] = {{100,100}, {300,100}, {300,300}, {100,300}};
  //vec_t c[] = {{100,300}, {300,300}, {300,100}, {100,100}};
  vec_t s[] = {	{50,150}, {200,50}, {350,150},
      {350,300},{250,300},{200,250},
      {150,350},{100,250},{100,200}};
#define clen (sizeof(c)/sizeof(vec_t))
#define slen (sizeof(s)/sizeof(vec_t))
  poly_t clipper = {clen, 0, c};
  poly_t subject = {slen, 0, s};
 
  poly res = poly_clip(&subject, &clipper);
 
  for (i = 0; i < res->len; i++)
    printf("%g %g\n", res->v[i].x, res->v[i].y);
 
  /* long and arduous EPS printout */
  FILE * eps = fopen("test.eps", "w");
  fprintf(eps, "%%!PS-Adobe-3.0\n%%%%BoundingBox: 40 40 360 360\n"
    "/l {lineto} def /m{moveto} def /s{setrgbcolor} def"
    "/c {closepath} def /gs {fill grestore stroke} def\n");
  fprintf(eps, "0 setlinewidth %g %g m ", c[0].x, c[0].y);
  for (i = 1; i < clen; i++)
    fprintf(eps, "%g %g l ", c[i].x, c[i].y);
  fprintf(eps, "c .5 0 0 s gsave 1 .7 .7 s gs\n");
 
  fprintf(eps, "%g %g m ", s[0].x, s[0].y);
  for (i = 1; i < slen; i++)
    fprintf(eps, "%g %g l ", s[i].x, s[i].y);
  fprintf(eps, "c 0 .2 .5 s gsave .4 .7 1 s gs\n");
 
  fprintf(eps, "2 setlinewidth [10 8] 0 setdash %g %g m ",
    res->v[0].x, res->v[0].y);
  for (i = 1; i < res->len; i++)
    fprintf(eps, "%g %g l ", res->v[i].x, res->v[i].y);
  fprintf(eps, "c .5 0 .5 s gsave .7 .3 .8 s gs\n");
 
  fprintf(eps, "%%%%EOF");
  fclose(eps);
  printf("test.eps written\n");
 
  return 0;
}

If the rectangle cuts off an integral part of the polygon, then everything works great. But what if the cut results in multiple polygons. For example, like this:

Coordinates

vec_t c[] = {{100,100}, {100,300}, {500,300}, {500,100}};
vec_t s[] = {{50, 200}, {50,350}, {200,450}, {250, 300}, {330, 220}, {150, 350}, {280, 200}};

The program gives the result as a single coordinate vector (more precisely, as a single polygon object). How to split coordinates by appropriate trims? (For example, to have the clipping function return an array of polygons rather than a single polygon.)

Answer 1

This program will not work on such polygons. There is a comment:
/* this works only if all of the following are true:
...
* 4. poly is convex (implying 3).
The above code works only for convex polygons, here even the problem is not that the truncated part is disconnected. There are simpler cases where the program will give the wrong answer.
I see such a solution to the problem - to intersect all edges with all edges and divide the edges by intersection points into several new ones. Mark edges in clockwise order around polygons. Then execute the closed area selection algorithm (described below). Then, in each area, separately check whether it is the intersection of both polygons (In this case, all edges will be in clockwise order).
Algorithm for selecting closed areas:
We build a directed graph, where the vertices are the vertices of the polygons (+ intersection points), and the edges are directed segments (instead of each segment, we create two edges in both directions between the vertices - the ends of the segment).
At each vertex, sort all outgoing edges by angle in a clockwise direction. Also, for each edge, when constructing, it is necessary to fill in the reverse edge.
Then we perform a bypass - From any edge that has not yet been passed, go to the next edge, going as far to the left as possible. To do this, we take the reverse edge and the next one from it in the sort order at the vertex. Roughly speaking, we drag our finger along the edges each time leaving the current area to the left of the edge. In such a traversal, we will bypass all the edges of the closed area and return to the initial edge. By running farther away from all unbypassed edges, we can select all areas.
There will be one extra outer area, but there the order of detour will be different and it will have the maximum area. It can be excluded by counting, for example, the areas of all regions. Or count with a sign and her sign is not the same, or modulo, then she is the largest and the sum of all the others.
Then, for all areas, we check that all the edges there are of the correct orientation (clockwise, like the original polygons). If it matches, then this area is the intersection of polygons.
It doesn't work if the polygons don't intersect. Then you need to check any point of each, whether it is contained entirely in the second polygon.