Can an image be reversibly decomposed into several, with a change in spatial frequency?

Question

Mathematics

I approached this topic not from mathematics and programming, but from the side of Photoshop and retouching. There is such a retouching technique - “ frequency decomposition method ”, when the image is divided into several layers so that small details are in one layer, medium in size in another, and very large, “low-frequency” ones in the third. At the same time, by overlaying these layers in the Linear Light mode on the lowest one, the original image is obtained. This is convenient: you can easily remove, for example, all the freckles from the model, because. they are in a separate layer. Layers are obtained by blurring one (becomes more low-frequency) and calculating the difference (Apply Image - Subtract (2, 128)) with the original one.
Now to my question. Is it possible to transform the original image into several intermediate ones, in which the contrasting edges completely disappear and are absent in all intermediate images? A normal blur will of course give this effect. But I'm interested in a reversible transformation: so that from these "blurred" ones you can then reassemble the original one with a sharp contrasting edge: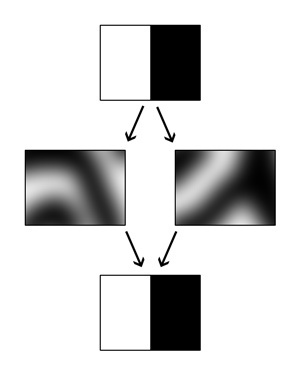

this is not a double-pixel image, but a large picture, like, with something very contrasting and clear)
Is this possible in principle?

Answer 1

Wavelet transform. It seems to be used in Jpeg-2000.

Answer 2

A tricky question, because it is not entirely clear what exactly is required. Generally speaking, this can be done on a Turing machine. To do this, you need to make a copy, blur the image, and then add the blurry image to the copy in some tricky reversible way (thousands of them). We get two blurry images, but by already simple manipulations we can restore them. You can use the spectral space to make everything fun from a mathematical point of view. However, the meaning of this undertaking eludes me.

Answer 3

If I understand correctly, clustering with a limitation on the size of clusters will help you more - an analogue of that transformation, but without working on the data. When blurring information is inevitably lost, this is an irreversible process.