Calculate the cross section of a color space ball?

Question

Design

A task from the field of color and palettes.
There is a three-coordinate color space CIE Lab.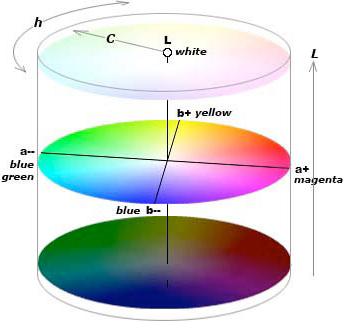

There is a figure, for example, a ball, which is a cut out local piece of the color space. Each of the dots in the ball is expressed by one of the three color components.
I want to calculate the sections of this ball with a two-dimensional plane, that is, get the colors of all the points of the resulting circle.
The plane relative to the ball has two parameters. Maybe you will express them more precisely, but at first glance they are:
1. The angle of contact (more precisely, two angles in spherical coordinates). Such a three-dimensional angle, which is formed between the center of the ball and the point of contact of the sphere with a plane parallel to the given one.
2. Removal from the center. The smallest distance from the section plane to the center of the ball.
Please tell me how to calculate such a cross section, i.e. how to find the 3D coordinates of its points.

Answer 1

Well, what exactly is the problem?
You have three coordinates: L, a, b. These are cylindrical (or spherical) coordinates. They can always be expressed in terms of rectangles (I think you know how). In rectangular coordinates, you set the plane in the position you need, for all points of this plane that are within the sphere (cylinder), translate the coordinate system, calculate the color.