[Automatic control theory] How to choose a formula to describe the probability distribution surface?

Question

higher mathematics

I ask for help in choosing a formula for describing the surface of the probability distribution.
The main difficulty is that various typical formulas can be used as a basis - parabola, hyperbola, sinusoid, sphere, etc.
The probability distribution surface will look similar to the image in the attached picture: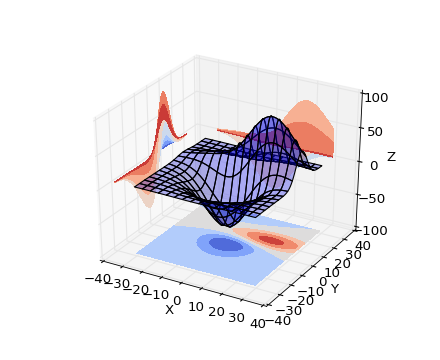

I.e. there will always be at least two peaks near the surface - positive and negative. They may vary in height and location. Each side of the X and Y axes can have their own negative and positive peaks.
To calculate the probability, we use the Bayesian probability, i.e. we have the ability to take into account the expectation of the occurrence of an event
. The experience has the following form (for the classic example of tossing a coin):
1. There is a mountain (mountain slope) at the base of which there is a concrete block. This is a "Coin Launcher".
2. There is a trolley that rolls down the slope and rests on a concrete block. This is "Coin".
Test conditions: The
trolley ALWAYS rests against a concrete block.
The minecart can stop on a concrete block and still not be damaged - this is the "Positive Peak" of the surface.
The cart can stop on a concrete block and completely collapse - this is the "Negative peak" of the surface.
The trolley can stop on a concrete block and partially collapse - these are other values ​​​​of the surface.
With a frequency of 1 sec. calculate the probability (i.e.
At a zero test step, i.e. before the first toss of a coin, the tester can choose the slope of the mountain, its steepness, terrain profile, size, etc.
In the process of testing, influence the "Installation for launching a coin", i.e. The tester cannot "mountain", or his influence tends to zero and can be neglected. The tester can have any influence on the "Setting for launching a coin" BEFORE testing, by selecting the parameters.
The tester can influence the physical characteristics of the Coin / Cart in such a way as to get as close as possible and, during the entire test, be in the area of ​​​​the positive peak.
Those. descending from the Mountain, the Tester can change the characteristics of the movement of the trolley (brake, tilt,
Because the main task is to stop the trolley with the least damage, then the actions of the Tester are subject to this particular task. Accordingly, if as a result of the Tester's actions the parameters shift towards a negative peak, then his actions should be aimed at changing the Coin / Cart in such a way as to move towards a positive peak, but these actions may not be successful.
-------------
For such an experience, I need to build a probability distribution surface.
How the probability distribution surface should look like - I indicated at the very beginning of the question.
What kind of formula would you recommend - hyperbola, parabola, sinusoid (when they rotate, they give cones that can be peaks)? Or does it make sense to use the equation of a sphere dissected by the plane of the XY axes and displaced relative to each other?
PS: It can be assumed that there will be three types of variable parameters - A - internal parameters of the system, B - external parameters of the system, C - control action of the Tester. But that's just my guess...

Answer 1

1 ) as far as I understood the presentation - the surface depicted by you
is not a probability density, but simply a certain objective function ) tell what your final goal is, then it will be possible to explain what kind of mathematical apparatus you need to use here; so far the tag "probability theory" is not very suitable here