Algorithm for finding empty rectangles?

Question

Mathematics

There is a field with filled squares and empty space. It is necessary to form visible rectangles from the empty space.
1. Field:

2. If you draw guides on the extreme sides of the visible squares, then a grid is formed: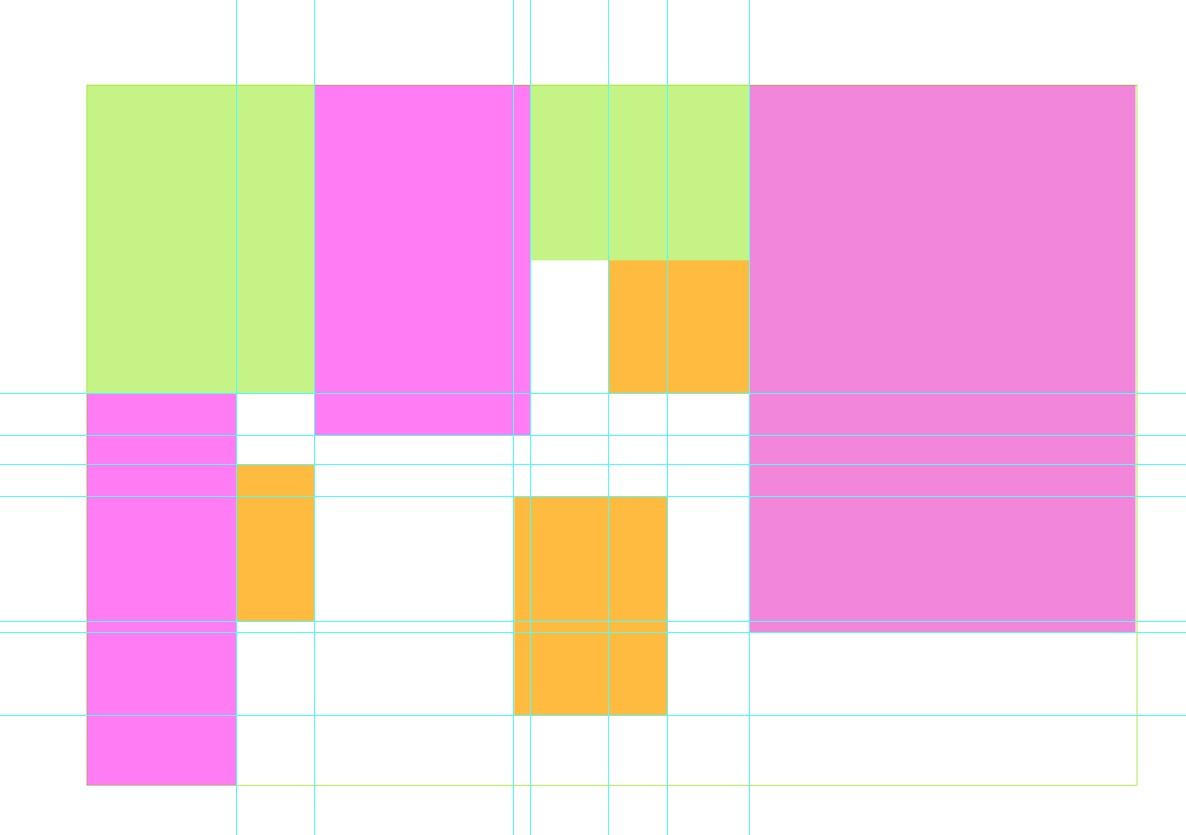

3. It is necessary to form the smallest number of solid rectangles from empty space:

4. For example, the image above can be split like this:

or so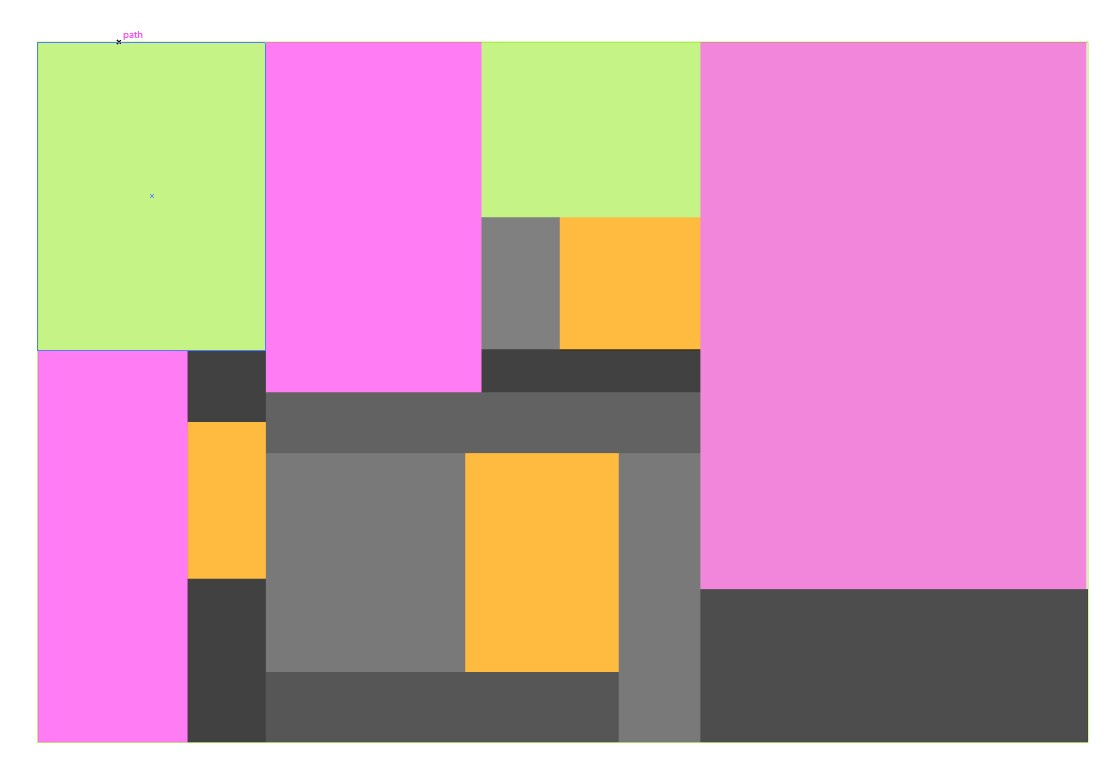

A can be and generally divided into many small rectangles at the intersection of the guides, but the task is to form as large rectangles as possible and, as a result, the smallest number of them.
What algorithm for such a task would be best suited (optimal in terms of speed)?

Answer 1

It seems to be simple. No NP-completeness.
Superficially it seems that this will result in the smallest possible number. However, area maximization is not guaranteed. Although, perhaps, such an approach may not find the best option when the boundaries of several source blocks lie exactly on the same line. Then the option that captures both voids wins. Imagine the silhouette of the letter "T". It can be tiled with just two rectangles. But the algorithm can miss this opportunity and offer 3 blocks.
Imagine an L-shaped set of blocks. Whatever one may say, there will be at least 2 in the end. Notice that in both options you got 9 rectangles.
P.2 in more detail. Various strategies are possible here. In particular:

• It is possible to "go" from the block in one direction, attaching neighbors, until it hits a non-empty area. Then try to expand to the second side with all the accumulated blocks, until it stops. Then the third and fourth.
  
• You can go in a spiral. 1 step up, 1 step right, 1 step down, 1 step left, etc. while 4 steps in a row, none will give an increase.
  

Answer 2

https://en.wikipedia.org/wiki/Covering_problems
Specifically: https://en.wikipedia.org/wiki/Polygon_covering#Cov...

Answer 3

In general, here I think such a course of action. test of the edge for proximity to the void ---> depending on the side that is adjacent, we form an array of visible blocks lying on its path and sort by the smallest coordinate (depending on the side, if the right side of the base block then sort what is on the right by x1, on the left by x2, etc.) ---> form a block and restart the cycle, mark each new block found ---> when the void ends, we run through the cycle all the marked found blocks for the possibility of merging. something like that probably

Answer 4

everything is very simple. from the beginning, we add rects to the entire field in a certain sheet of nodes. then we run through all rects that are on the field, let it be CurrentRect, and for each we execute the algorithm:
we run through all nodes from i = 0 to nodes.Count - 1 (during the run, nodes.Count can change)
{
Take nodes[i ] and if it intersects with CurrentRect (it intersects and does not touch) we do the following:
{
Trim it along CurrentRect. how exactly: from the beginning from the bottom, if there is something to cut, we shove a new rect into the nodes and cut the current one along the CurrentRect, and so on all sides
We remember the first one in the run as the main one, which will eventually remain in the place of the CurrentRect, if it is less than the CurrentRect, we stretch it along CurrentRect.
After the cuts, we delete all the rest (the pieces that will lie in the CurrentRect, they are superfluous) and do i--
}
}
Then we can do optimization, find rects with the same faces and merge them. You can also come up with something else. But this is an easier task